Polyèdres Uniformes
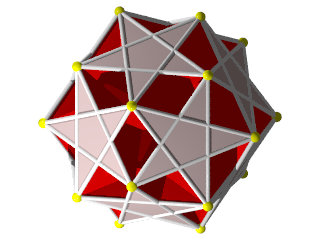
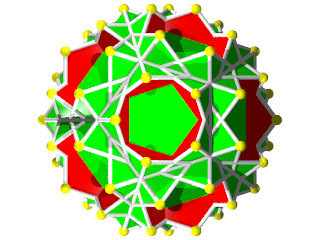
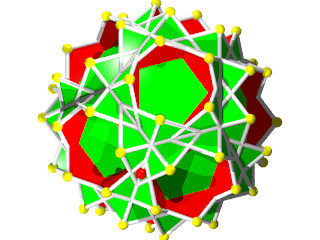
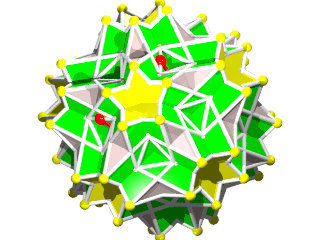
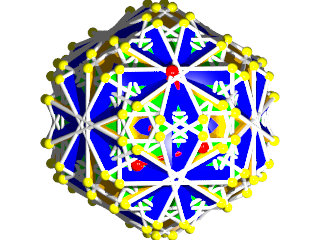
Comme Jean-Jacques Dupas le disait sur sa page des Polyèdres, il est fasciné par les polyèdres uniformes, voici donc un article réalisé par Jean-Jacques Dupas consacré aux polyèdres uniformes. Cet article n'engage que son auteur.
C'est l'article est le plus complet du Web sur le sujet. Tout ce que vous voulez savoir sur les polyèdres uniformes sans avoir jamais osé le demander!
Rappelons qu'un polyèdre uniforme est un polyèdre constitué de polygones réguliers (au sens large, les étoiles sont permises) tel qu'il existe des isométries pouvant transformer un sommet quelconque en tous les autres (c'est-à-dire qu'un sommet se présente toujours de la même façon, ce que l'on représente par la figure de sommet)
Les images seront :
- des photos d'un vrai polyèdre que j'ai construit (ces photos sont copyright Jean-Jacques Dupas 2015)
- des photos de polyèdres réalisés sur des imprimantes 3D du fab lab de Ris-Orangis par Olivier de Planète-Science (ces photos sont copyright Jean-Jacques Dupas 2015)
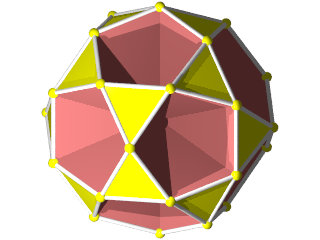
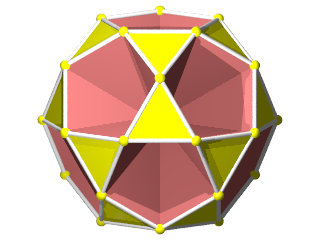
- des images de synthèse que j'ai réalisées avec le logiciel PovRay (ces photos sont copyright Jean-Jacques Dupas 2015)
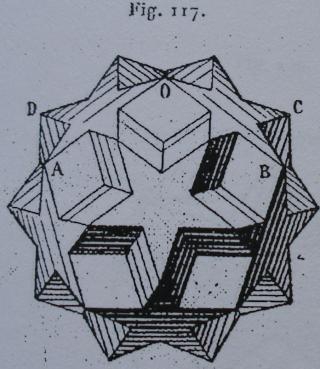
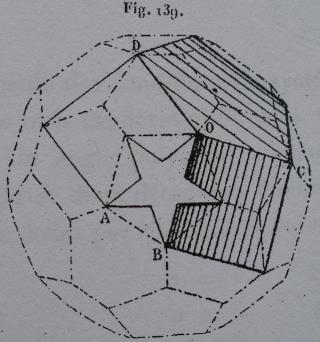
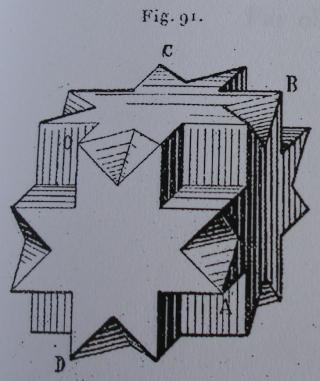
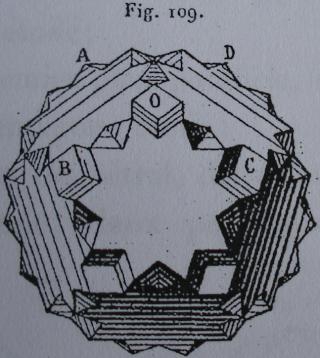
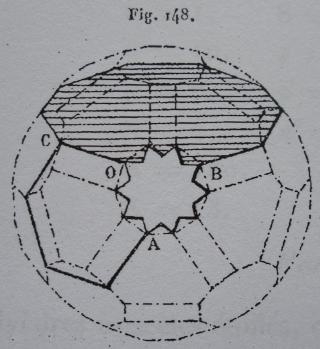
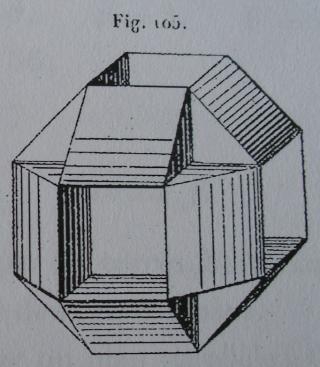
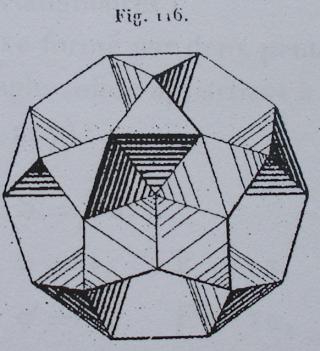
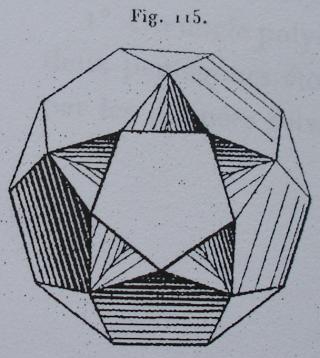
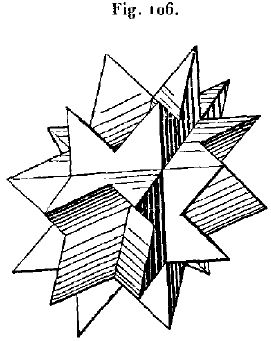
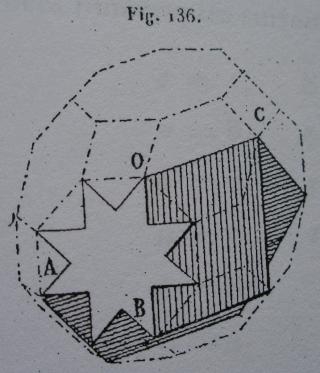
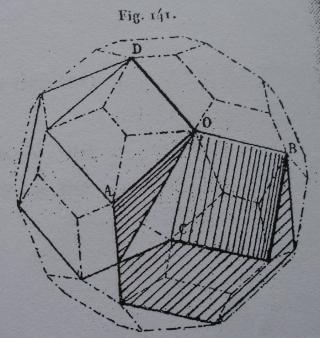
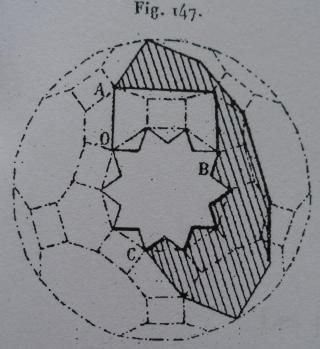
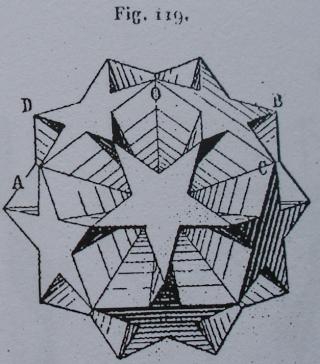
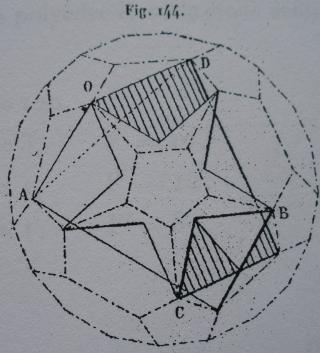
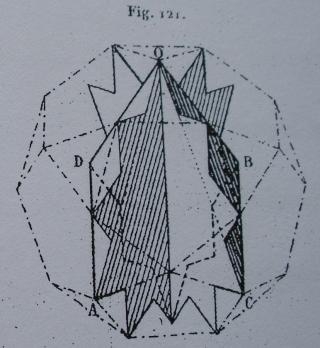
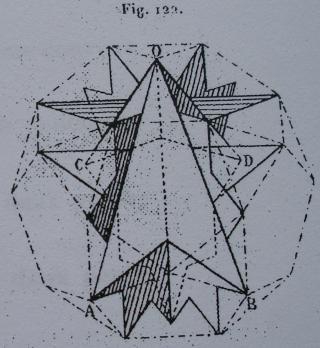
- des images tirées du mémoire d'Albert Badoureau (1853-1923) "Mémoire sur les figures isoscèles", Journal de l'École Polytechnique 49 (1881) 47-1727
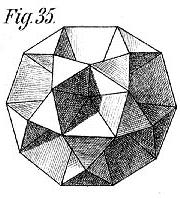
- des images tirées du livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Pour la description des polyèdres je me réfère à la numérotation de mon ami Magnus Wenninger et de son livre Polyhedron Models
Les polyèdres uniformes non convexes, hors étoiles de Kepler-Poinsot, prismes et antiprismes (les polyèdres uniformes convexes étant les solides de Platon, les solides archimédiens, les prismes réguliers convexes et les antiprismes réguliers convexes) se rangent en deux catégories :
Les polyèdres uniformes réflexifs (de W67 à W109). Ils sont générés par le groupe de symétrie complet, Ils possèdent tous les plans de symétrie du système de symétrie, ils sont constructibles à la règle et au compas, d'ailleurs ceux que j'ai construits l'ont été sans aucun calcul, juste avec un peu de géométrie descriptive. Ils ont été presque tous découverts par Albert Badoureau sa technique aurait pu lui permettre de découvrir tous les polyèdres uniformes réflexifs.
- Ceux à symétrie tétraédrique (il n'y en a qu'un) sont composés de triangles et carrés
- Ceux à symétrie octaédrique sont composés de triangles, carrés, hexagones, octogones, étoiles à huit branches
- Ceux à symétrie icosaédrique sont composés de triangles, carrés, pentagones, hexagones, décagones, pentagrammes, étoiles à dix branches
Les polyèdres uniformes camus (de W110 à W118) Ils sont générés par le groupe de symétrie de rotation, un sous-groupe du groupe complet, Ils ne possèdent pas en général de plans de symétrie (sauf le W110 et W118), ils ne sont pas constructibles à la règle et au compas, d'ailleurs ceux que j'ai construits l'ont été par le calcul.
Le W119 possèdent d'autres particularités, il ne peut pas être construit par la méthode de Wythoff, comme il possède des propriétés proches des camus on le range généralement dans la catégorie des camus.
Sommaire
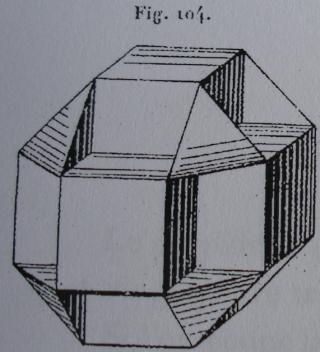
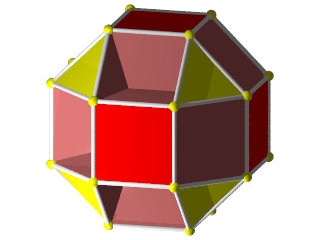
W67
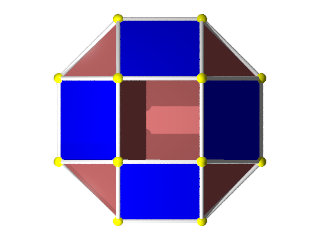
TétraHémiHexaèdre Wikipédia
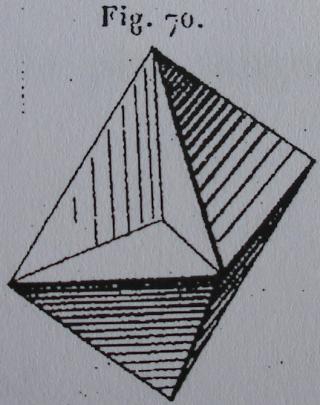
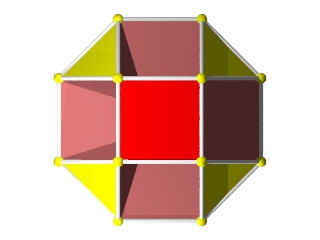
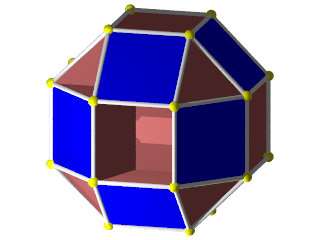
Un TétraHémiHexaèdre à gauche à côté d'un octaèdre à droite
Hémi signifie que les 6 faces carrées du cuboctaèdre se sont rapprochées pour ne plus constituer que les 3 carrés équatoriaux de l'octaèdre.
Donc Hémi Hexaèdre nous dit que l'on n'a que la moitié des 6 faces d'un cube (en fait les 6 faces carrées d'un cuboctaèdre)
Le Tétra fait sans doute référence à la symétrie tétraédrique.
Ce solide est le seul polyèdre uniforme non convexe de symétrie tétraédrique.
Ce solide a été décrit la première fois par Albert Badoureau en 1881 qui l'a baptisé semi-octaèdre.
Notez l'antériorité sur Reinhardt (1885).
Dans le livre Les polyèdres réguliers, semi-réguliers et composés Louis Joly attribue ce polyèdre à Curt Reinhardt (l'heptaèdre de Reinhardt).
Ce polyèdre est non-orientable et est le seul polyèdre uniforme avec un nombre impair de faces 7 d'où son nom d'heptaèdre.
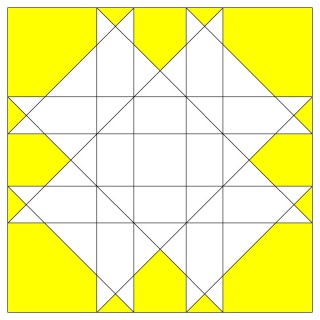
La construction:
On prépare un carré complet, au centre, deux demi carrés à droite, quatre quarts de carré à gauche et 4 triangles en bas.
On assemble un demi carré sur la diagonale d'un carré. Notez qu'une languette est à gauche sur le carré et l'autre à droite.
On assemble un deuxième demi carré sur la diagonale d'un carré.
Puis on assemble les quarts de carré. On colle les languettes des triangles ensemble.
Il n'y a plus qu'à coller les triangles et on obtient ce premier polyèdre uniforme, facile non ?
Quelques données sur ce polyèdre:
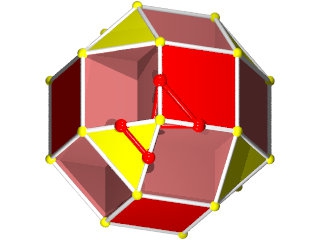
Possède les mêmes sommets qu'un octaèdre
Possède les mêmes arêtes qu'un octaèdre
Faces : 4{3}+3{4}
Sommets: 8
Symbole de Wythoff 3/2 3 | 2
Rayon de la sphère circonscrite Racine de 2 pour une arête de longueur 2
Références :
p.101-102 de Polyhedron Models
p.95 de Shapes, Space and Symmetry, Alan Holden, Dover
p.46-47 Les polyèdres réguliers, semi-réguliers et composés
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 36
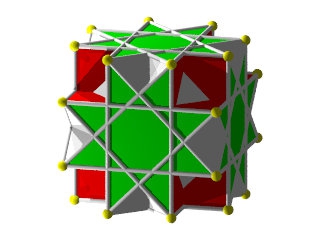
W68
OctaHémiOctaèdre Wikipédia
Symétrie octaédrique
Hémi signifie que les 8 faces hexagonales du grand rhombicuboctaèdre se sont rapprochées pour ne plus constituer que les 4 hexagones équatoriaux du cuboctaèdre. Le premier octa fait référence aux 8 faces triangulaires de l'octaèdre
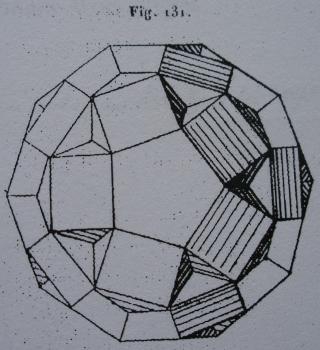
Ce solide a été décrit la première fois par Albert Badoureau en 1881
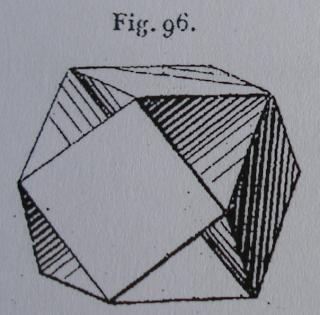
On le trouve également dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Le W68
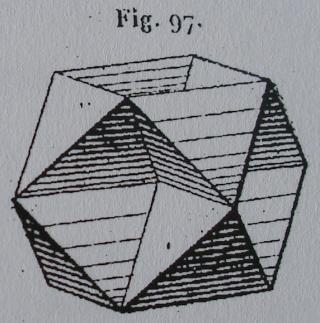
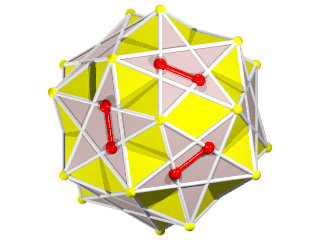
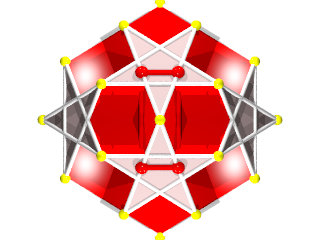
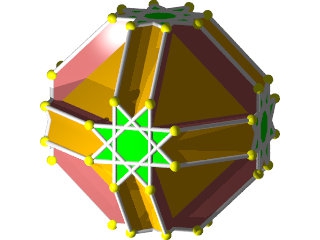
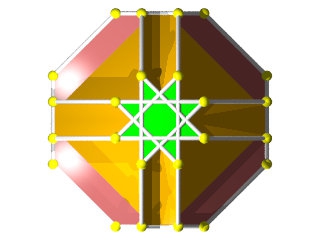
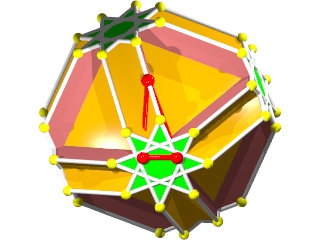
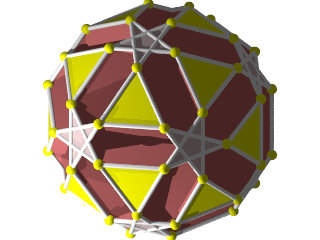
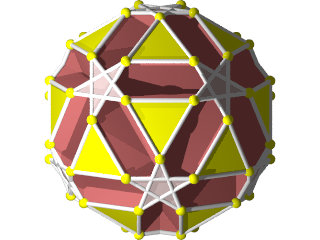
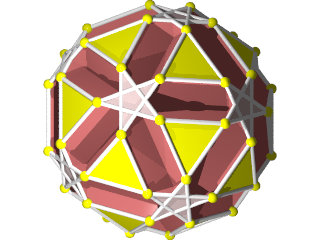
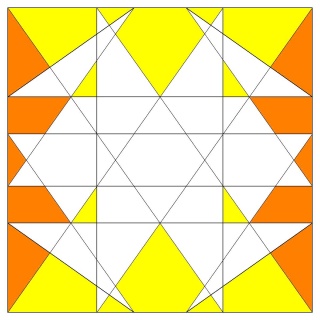
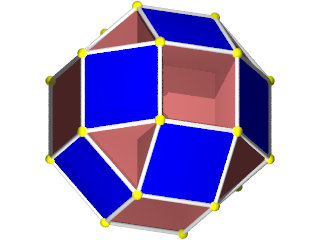
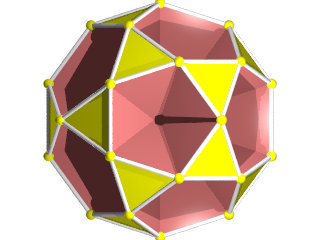
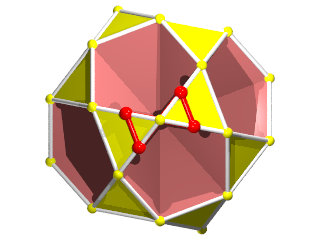
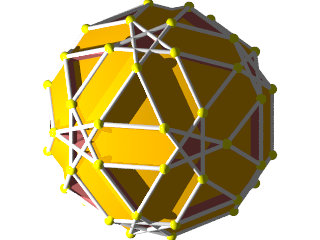
Le W68 vu d'une face triangulaire ou hexagonale
Le W68 vu d'un sommet
Le W68 et sa figure de sommet
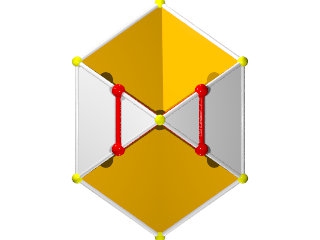
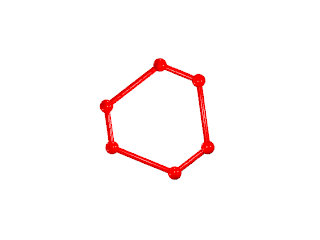
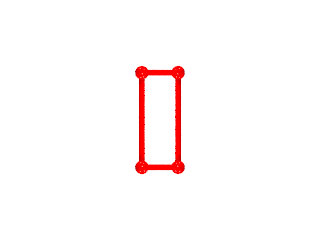
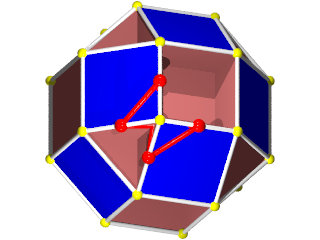
La figure de sommet du W68 seul (les grandes barres sur des {6} et les petites sur des {3})
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un cuboctaèdre
Possède les mêmes sommets qu'un cuboctaèdre et qu'un W78
Possède les mêmes arêtes qu'un cuboctaèdre
Possède les mêmes faces triangulaires qu'un cuboctaèdre
Possède les mêmes faces hexagonales qu'un W78
Faces : 8{3}+4{6}
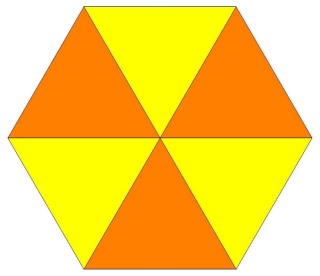
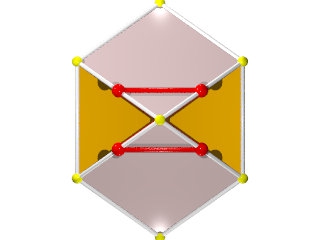
Le triangle est vu en entier
Par contre l'hexagone équatorial est vu tantôt dessus en jaune, tantôt dessous en orange
Sommets: 12
Symbole de Wythoff 3/2 3 | 3
Rayon de la sphère circonscrite 2 pour une arête de longueur 2 comme le W78
Références :
p.103 de Polyhedron Models
p.96 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 37
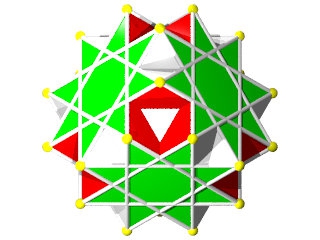
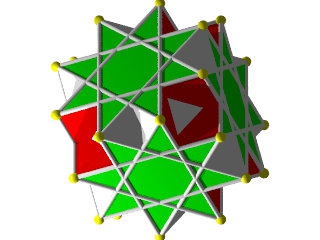
W69
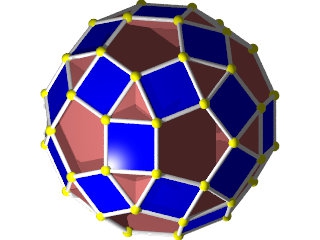
Petit Cubicuboctaèdre ( Wikipédia )
Les faces carrées sont celles d'un cube d'où cubi
et il y a 8 faces triangulaires et 6 faces carrées comme dans cuboctaèdre
Symétrie octaédrique
Un polyèdre inscrit dans un petit rhombicuboctaèdre
Ce solide n'est pas très spectaculaire, il ressemble trop au petit rhombicuboctaèdre, il n'est cependant pas très long à construire 62 pièces
Ce solide a été décrit la première fois par Albert Badoureau en 1881
On le trouve également dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900) sous une forme moins régulière
Le W69
Le W69 vu d'une face carrée ou octogonale
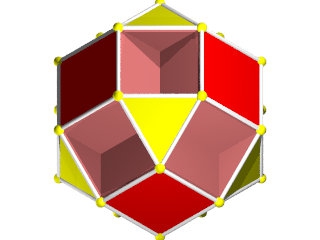
Le W69 vu d'une face triangulaire
Le W69 vu d'un sommet
Le W69 et sa figure de sommet
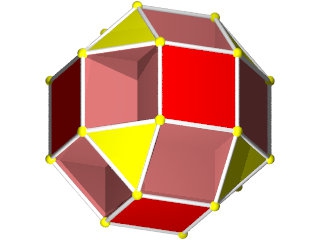
La figure de sommet du W69 seule, le carré la barre en haut à droite, le triangle en bas à gauche et les deux octogones qui se croisent.
Le triangle est vu en entier
Le carré est aussi vu en entier
Par contre l'octogone est vu partiellement par dessus en jaune et par dessous en orange
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un petit rhombi-cuboctaèdre
Il possède les mêmes sommets qu'un petit rhombi-cuboctaèdre et qu'un W92 mais pas de même rayon circonscrit.
Il possède les mêmes sommets qu'un petit rhombi-cuboctaèdre, qu'un W86 et qu'un W92 de même rayon circonscrit.
Il possède les mêmes arêtes qu'un petit rhombi-cuboctaèdre
Il possède les mêmes faces carrées et triangulaires qu'un petit rhombi-cuboctaèdre
Il possède les mêmes faces octogonales qu'un W86
Faces : 8{3}+6{4}+6{8}
Sommets: 24
Arêtes : 48
Symbole de Wythoff 3/2 4 | 4
Rayon de la sphère circonscrite Racine de (5 + 2 Racine de deux) pour une arête de longueur 2 comme le W86
Références :
p.104-105 de Polyhedron Models
p.97 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 38
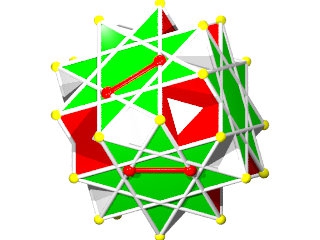
W70
Petit Icosidodécaèdre Ditrigonal ( Wikipédia )
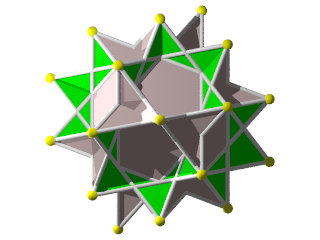
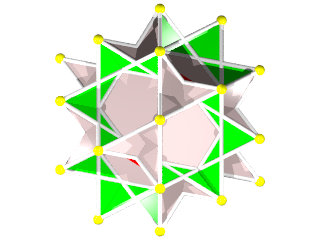
Symétrie icosaédrique
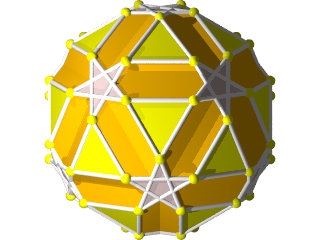
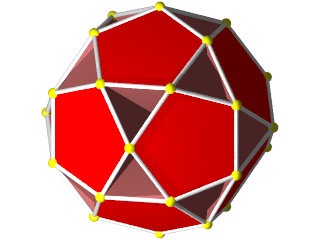
C'est un charmant polyèdre facile à construire 72 pièces et assez spectaculaire avec ses 12 pentagrammes.
Ce polyèdre est inscrit dans un dodécaèdre régulier.
Les pentagrammes sont inscrits dans les pentagones du dodécaèdre.
Les 20 triangles sont ceux d'un icosaèdre.
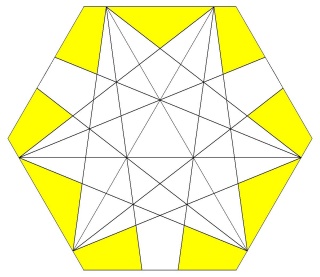
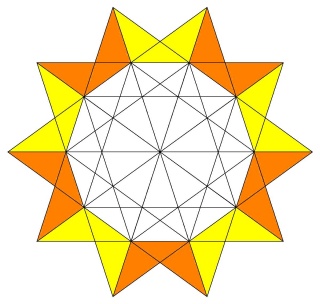
autour de chaque sommet on rencontre alternativement pentagramme triangle comme dans un icosidodécaèdre et ceci 3 fois d'où son nom de petit icosidodécaèdre ditrigonal
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J. Pitsch en 1881.
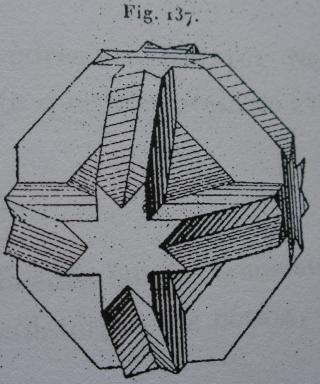
On le trouve également dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Le W70
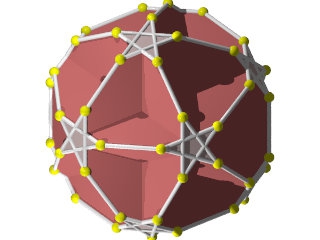
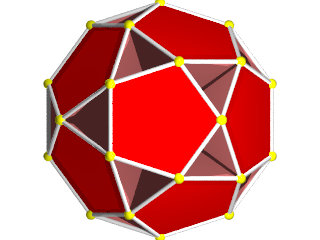
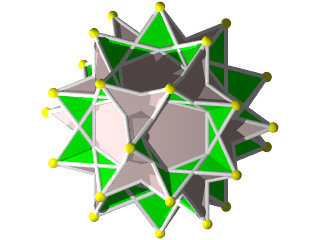
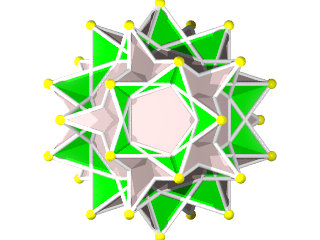
Le W70 vu d'une face triangulaire
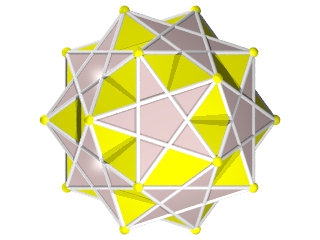
le W70 vu d'une face en forme de pentagramme
Le W70 vu d'un sommet
Le W70 et sa figure de sommet
La figure de sommet du W70, pentagramme, triangle, pentagramme, triangle, pentagramme, triangle.
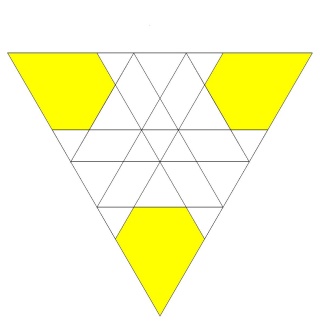
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un dodécaèdre régulier
Il possède les mêmes sommets qu'un dodécaèdre régulier
Il possède les mêmes arêtes qu'un W87 , W80 et que 5 cubes inscrits dans un dodécaèdre régulier
Il possède les mêmes faces triangulaires qu'un W87
Il possède les mêmes faces en forme de pentagramme qu'un W80
Faces : 20{3}+12{5/2}
les pentagrammes sont vus en entier
Par contre les triangles sont partiellement visibles
Sommets: 20
Arêtes : 60
Symbole de Wythoff 3 | 3 5/2
Rayon de la sphère circonscrite Racine de 3 pour une arête de longueur 2 comme le W80 et W87
Références :
p.106-107 de Polyhedron Models
p.100 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 39
W71
Petit icosicosidodécaèdre ( Wikipédia )
Symétrie icosaédrique
20 Triangles et 12 pentagrammes ce qui fait penser à un icosidodécaèdre et les 20 triangles externes font penser à un icosaèdre.
Un modèle assez facile à faire 92 pièces.
Ce polyèdre est inscrit dans un Petit rhombicosidodécaèdre modifié, il a été oublié par Badoureau.
Ce solide a été décrit la première fois par J.Pitsch en 1881.
par contre on le trouve dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900).
Le W71.
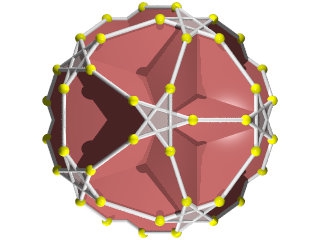
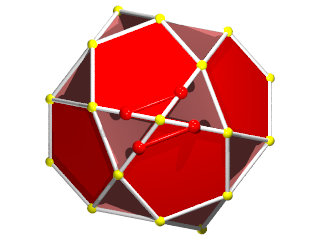
Le W71 vu d'une face triangulaire.
Le W71 vu d'une face pentagonale.
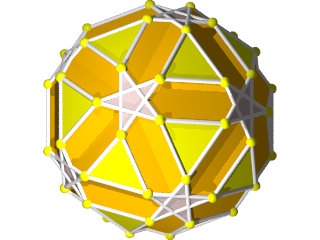
Le W71 vu d'un sommet.
Quelques données sur ce polyèdre :
ce polyèdre est inscrit dans un petit rhombicosidodécaèdre irrégulier.
Il possède les mêmes sommets que le W104 mais pas le même rayon circonscrit.
Il possède les mêmes sommets que le W82 et le W90 avec le même rayon circonscrit.
Il possède les mêmes arêtes que le W82 et le W90.
Il possède les mêmes faces triangulaires et en forme de pentagrammes que le W82.
Il possède les mêmes faces hexagonales que le W90.
Faces : 20{3}+20{6}+12{5/2}
Les pentagrammes sont vus en entier
ainsi que les triangles
Alors que les hexagones sont partiellement vus.
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5/2 | 3
Rayon de la sphère circonscrite Racine de ((17+3 Racine(5)/2) pour une arête de longueur 2
Références :
p.108-109 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 40
W72
Petit dodécicosidodécaèdre ( Wikipédia )
Symétrie icosaédrique
20 triangles et 12 pentagones comme un icosidodécaèdre et 12 décagones dans les plans d'un dodécaèdre.
162 pièces donc un polyèdre non trivial pour un résultat trop proche d'un petit rhombicosidodécaèdre.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Il semble qu'il ne soit pas décrit par Brückner.
Un W72
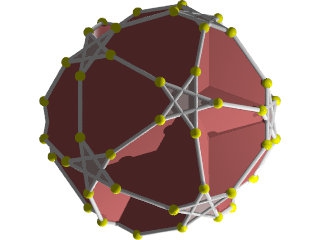
Un W72 vu d'une face triangulaire
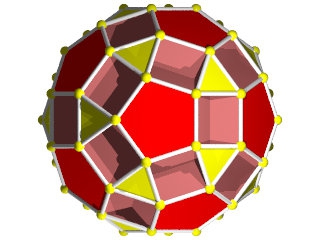
un W72 vu d'une face pentagonale
le W72 vu d'un sommet
Le W72 et sa figure de sommet
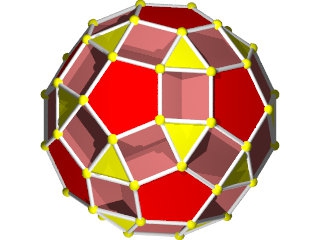
La figure de sommet du W72, pentagone en haut à droite, triangle en bas à droite et décagones qui se croisent.
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un petit rhombicosidodécaèdre régulier
Il possède les mêmes sommets qu'un petit rhombicosidodécaèdre régulier, qu'un W74 avec le même rayon circonscrit.
Il possède les mêmes sommets qu'un petit rhombicosidodécaèdre régulier, qu'un W97 avec un rayon circonscrit différent.
Il possède les mêmes arêtes qu'un petit rhombicosidodécaèdre et un W74.
Il possède les mêmes faces triangulaires et pentagonales qu'un petit rhombicosidodécaèdre.
Il possède les même faces décagonales qu'un W74.
Faces : 20{3}+12{10}+12{5}
Les triangles sont vus en entier
ainsi que les pentagones
Les décagones sont coupés et vus de dessus en jaune ou dessous en orange (quoique le dessus et le dessous n'aient pas beaucoup de sens, sans dessus-dessous une allusion à Badoureau ! )
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3/2 5 | 5
Rayon de la sphère circonscrite Racine de (11+4 Racine(5)) pour une arête de longueur 2 comme le W74
p.110-111 de Polyhedron Models
p.97de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 42
W73
Dodécadodécaèdre ( Wikipédia )
Symétrie icosaédrique
12 pentagones donc un dodécaèdre et 12 étoiles dans les plans des pentagones d'un dodécaèdre
Ce polyèdre est facile à construire 72 pièces et étonnant par sa régularité, sa simplicité, les creux constitués de losanges font un effet d'optique et semblent aller vers l'avant
Ce solide a été décrit la première fois par Albert Badoureau en 1881
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on le trouve dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
un W73
Un W73 vu d'un pentagramme
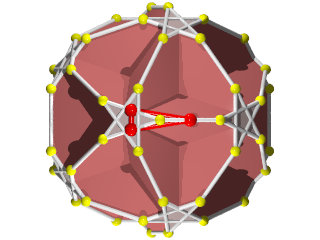
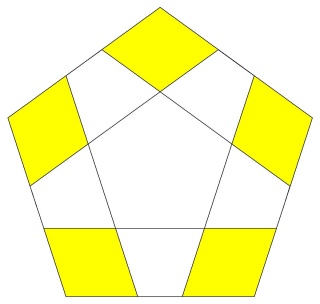
Un W73 vu d'un sommet
Le W73 et sa figure de sommet
La figure de sommet du W73 alternance de pentagones et pentagrammes, figure de sommet caractéristique d'un polyèdre quasi-régulier, d'ailleurs ce polyèdre possède des hexagones équatoriaux
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosidodécaèdre
Il possède les mêmes sommets qu'un icosidodécaèdre, W100 et W102
Il possède les mêmes arêtes qu'un W100, W102
Il possède les mêmes faces en forme de pentagramme qu'un W100
Il possède les mêmes faces pentagonales qu'un W102
Faces : 12{5}+12{5/2}
Les pentagrammes sont vus en entiers
Alors que les pentagones sont coupés.
Sommets: 30
Arêtes : 60
Symbole de Wythoff 2 | 5/2 5
Rayon de la sphère circonscrite 2 pour une arête de longueur 2 comme le W100 et le W102.
p.112 de Polyhedron Models
p.103 de Shapes, Space and Symmetry, Alan Holden, Dover
p.123 de Mathematical Models, Cundy Rollett, Tarquin
p.101 de Regular Polytopes, H.M.S. Coxeter, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 45
W74
Symétrie icosaédrique ( Wikipédia )
Petit rhombidodécaèdre
12 décagones dans les plans d'un dodécaèdre plus 30 carrés supplémentaires (des rhombes suivant l'expression de Kepler)
162 pièces donc un polyèdre non trivial ! Des morceaux ne tiennent que par des arêtes donc modèle difficile pour un résultat trop proche d'un petit rhombicosidodécaèdre
Ce solide a été décrit la première fois par Albert Badoureau en 1881
on le trouve dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
un W74
un W74 vu d'une face carrée
Un W74 vu d'une face décagonale
un W74 vu d'un sommet
Un W74 et sa figure de sommet
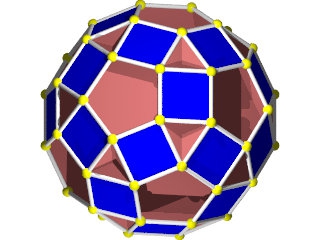
La figure de sommet du W74 seule, carré, décagones, carré décagones, les décagones sont croisés
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un petit rhombicosidodécaèdre régulier
Il possède les mêmes sommets qu'un petit rhombicosidodécaèdre régulier, un W72 et un W97
Il possède les mêmes arêtes qu'un petit rhombicosidodécaèdre et un W72
il possède les mêmes faces carrées qu'un petit rhombicosidodécaèdre
il possède les mêmes faces décagonales qu'un W72
Faces : 30{4}+12{10}
Les carrés sont vus en entier
alors que les décagones sont coupés et vus tantôt dessus en jaune et dessous en orange
Sommets: 60
Arêtes : 120
Symbole de Wythoff 2 5 (3/2 5/2)| 5
Rayon de la sphère circonscrite Racine de (11+4Racine(5)) pour une arête de longueur 2 comme le W72
p.113 de Polyhedron Models
p.97de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 46
W75
Grand dodécaèdre tronqué ( Wikipédia )
Symétrie icosaédrique
C'est une version tronquée du grand dodécaèdre ci-dessous
72 pièces assez facile à construire mais pas très spectaculaire !
Ce polyèdre a été oublié par Albert Badoureau il est inscrit dans un icosaèdre tronqué non régulier
Il est curieux de constater que Badoureau n'a pas travaillé à partir des solides de Kepler-Poinsot
Ce solide a été décrit la première fois par J.Pitsch en 1881
on le trouve dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
un W75
un w75 vu d'un pentagramme
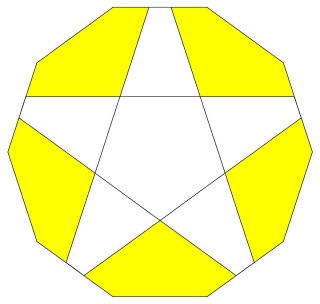
Un W75 vu d'un sommet
Le W75 et sa figure de sommet
La figure de sommet du W75 deux décagones les grands côtés et un pentagramme le petit côté.
Ce polyèdre a été oublié par Albert Badoureau, il est inscrit dans un icosaèdre tronqué non régulier
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier
Il possède les mêmes sommets qu'un W105, W99, W109 de rayon circonscrit différent
Faces : 12{10}+12{5/2}
Les pentagrammes sont vus en entier
Alors que les décagones sont coupés
Sommets: 60
Arêtes : 90
Symbole de Wythoff 2 5/2 | 5
Rayon de la sphère circonscrite Racine de ((17+ 5 Racine(5)) / 2) pour une arête de longueur 2
p.115 de Polyhedron Models
p.102 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 47
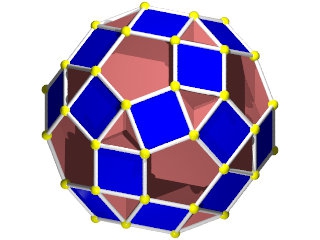
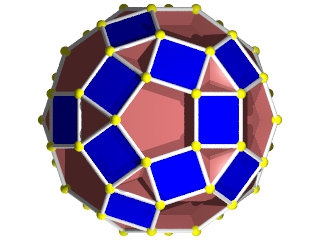
W76
Rhombidodécadodécaèdre ( Wikipédia )
Symétrie icosaédrique
12 pentagones comme un dodécaèdre, 12 pentagrammes dodéca et 30 carrés (les rhombes chers à Kepler)
Le premier polyèdre un peu complexe que j'ai construit, il m'a fallu deux mois pour le finir : 312 pièces la difficulté provient de la différence de taille des pièces et qu'il faut aligner 3 morceaux aussi bien pour les carrés que pour les pentagones, mais au final un superbe modèle !
Ce solide a été décrit la première fois par Albert Badoureau en 188.
Son dessin est assez partiel mais même pour un as de la géométrie descriptive comme l'était Albert Badoureau un dessin complet n'est pas une tâche aisée.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on le trouve dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W76
Un W76 vu d'une face carrée
un W76 vu d'une face pentagonale
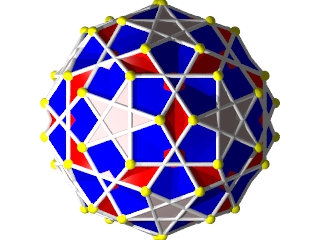
Un W76 vu d'un sommet
Le W76 et sa figure de sommet
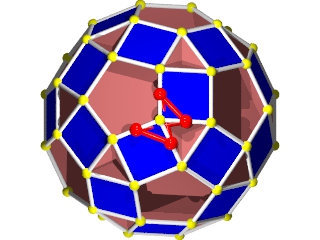
la figure de sommet du W76
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier
Il possède les mêmes sommets qu'un W83 et qu'un W96
Il possède les mêmes arêtes qu'un W83, W96
Il possède les mêmes faces pentagonales et en forme de pentagramme qu'un W83
Il possède les mêmes faces carrées qu'un W96
Faces : 30{4}+12{5}+12{5/2}
les pentagrammes sont vus en entier
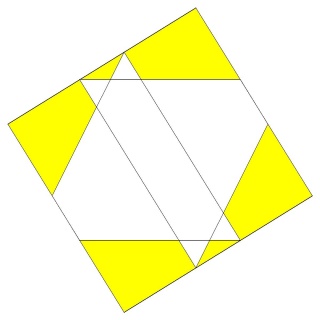
alors que les carrés sont coupés
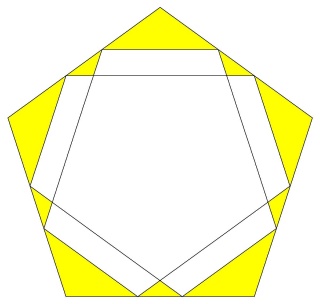
les pentagones aussi
Sommets: 60
Arêtes : 120
Symbole de Wythoff 5/2 5 | 2
Rayon de la sphère circonscrite Racine de (7) pour une arête de longueur 2 comme pour le W83 et le W96
p.116-117 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 48
W77
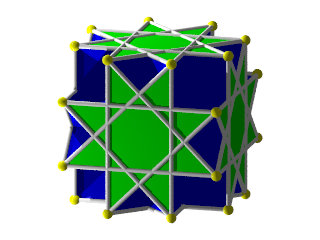
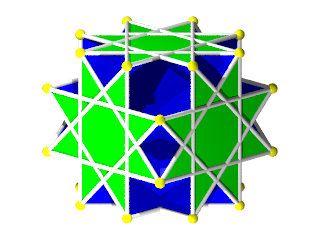
Grand cubicuboctaèdre ( Wikipédia )
symétrie octaédrique
8 triangles et 6 carrés comme un cuboctaèdre et 6 étoiles à 8 branches dans les plans d'un cube
Un modèle très facile à construire 62 pièces et que moi je trouve très sympa ! j'avais fait une maquette en papier, un de mes premiers polyèdres uniformes.
Remarquez que les modèles de la symétrie octaédrique comportent moins de pièces.
Ce solide a été décrit la première fois par Albert Badoureau en 1881
son dessin comporte des erreurs même un as de la géométrie descriptive comme Albert Badoureau peut se tromper, ne soyez pas moqueurs car Badoureau était un génie.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
un W77
Un W77 vu d'une face d'étoile
Un W77 vu d'un triangle
Un W77 vu d'un sommet
Un W77 et sa figure de sommet
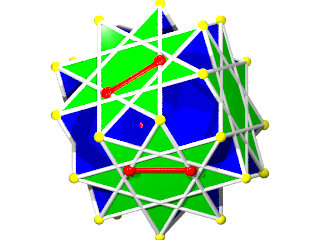
La figure de sommet d'un W77 seule
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un cube tronqué
Il possède les mêmes sommets qu'un cube tronqué, un W103 et un W85
Il possède les mêmes arêtes qu'un W85 et un W103
Il possède les mêmes faces carrées et triangulaires qu'un W103
Il possède les mêmes faces en forme d'étoile à 8 branches qu'un W85
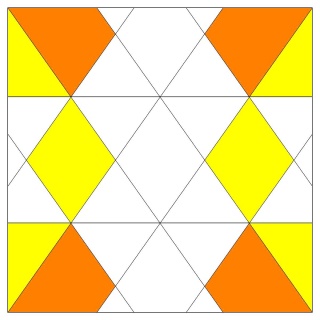
Faces : 8{3}+6{4}+6{8/3}
Les étoiles à 8 branches sont entières
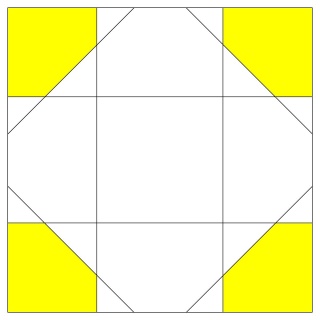
Alors que les carrés sont coupés
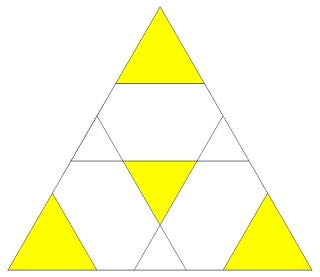
Ainsi que les triangles
Sommets: 24
Arêtes : 48
Symbole de Wythoff 3 4 | 4/3
Rayon de la sphère circonscrite Racine de (5-2Racine(2)) pour une arête de longueur 2 comme le W103 et le W85
p.118-119 de Polyhedron Models
p.108 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 50
W78
CuboHémiOctaèdre ( Wikipédia )
des hexagones équatoriaux par moitié d'où hémiOctaèdre et 6 faces carrées d'où le cubo
Symétrie octaédrique
A priori avec 30 pièces ce polyèdre ne devrait pas être trop difficile à construire, mais avec les hexagones équatoriaux il est plus difficile qu'il n'y parait pour un résultat très proche du cuboctaèdre
Ce solide a été décrit la première fois par Albert Badoureau en 1881
Un W78
un W78 vu d'une face carrée
un W78 vu d'une face hexagonale
Un W78 vu d'un sommet
Un W78 et sa figure de sommet
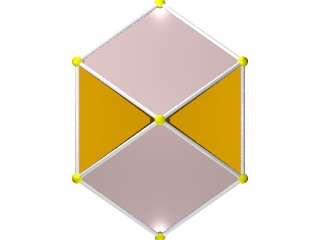
La figure de sommet d'un W78 seule
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un cuboctaèdre
Possède les mêmes sommets qu'un cuboctaèdre et qu'un W68
Possède les mêmes arêtes qu'un cuboctaèdre
Possède les mêmes faces carrées qu'un cuboctaèdre
Possède les mêmes faces hexagonales qu'un W68
Faces : 4{6}+6{4}
Les hexagones équatoriaux sont vus tantôt dessus en jaune, tantôt dessous en orange
Les carrés sont vus en entier
Sommets: 12
Arêtes : 24
Symbole de Wythoff 4/3 4 | 3
Rayon de la sphère circonscrite 2 pour une arête de longueur 2 comme le W68
Références :
p.120 de Polyhedron Models
p.96 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 51
W79
W79 Cuboctaèdre cubitronqué ( Wikipédia )
Symétrie octaédrique
Un polyèdre assez facile à réaliser, 62 pièces et assez original.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881.
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900).
Un W79
Un W79 vu d'une face octogonale
Un W79 vu d'une face hexagonale
un W79 vu d'un sommet
Un W79 et sa figure de sommet
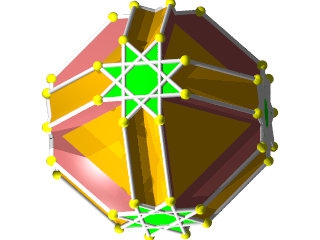
la figure de sommet du W79 seule
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un grand rhombi cuboctaèdre irrégulier
Faces : 8{6}+6{8}+6{8/3}
Les étoiles à 8 branches sont vus en entier
Alors que les octogones sont coupés
Ansi que les hexagones
Sommets: 48
Arêtes : 72
Symbole de Wythoff 3 4/3 4 |
Rayon de la sphère circonscrite racine(7) pour une arête de longueur 2.
Références :
p.121-122 de Polyhedron Models
p.105 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 52
W80
Ditrigonal Dodécadodécaèdre
symétrie icosaèdrique
12 pentagones comme un dodécaèdre, 12 pentagrammes 3 alternances de pentagrammes pentagones autour de chaque sommet d'où ditrigonal
Un modèle assez difficile, 192 pièces, il faut faire les pentagrammes les plus grands possibles, pour pouvoir construire les cavités très profondes bref une grand complexité assez invisible!
Ce solide a été décrit la première fois par Albert Badoureau en 1881. Sur son schéma il a juste indiqué comment construire le solide.
Un W80
Un W80 vu d'une face pentagonale
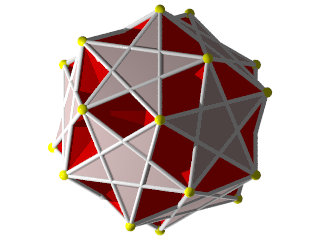
Un W80 vu d'un sommet
Le W80 et sa figure de sommet
La figure de sommet du W80
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un dodécaèdre régulier
Il possède les mêmes sommets qu'un dodécaèdre régulier
Il possède les mêmes arêtes qu'un W87, W70 et que 5 cubes inscrits dans un dodécaèdre régulier
Il possède les mêmes faces pentagonales qu'un W87
Il possède les mêmes faces en forme de pentagramme qu'un W70
Faces : 12{5}+12{5/2}
les pentagrammes sont vus en entier
Les pentagones sont coupés et vus dessus en jaune et dessous en oranges
Sommets: 20
Arêtes : 60
Symbole de Wythoff 3 | 5/2 5
Rayon de la sphère circonscrite Racine de 3 pour une arête de longueur 2 comme le W70 et le W87
Références :
p.123-124 de Polyhedron Models
p.101 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 53
W81
Grand dodécicosidodecaèdre ditrigonal ( Wikipédia )
Symétrie icosaédrique
20 triangles et 12 pentagones comme dans un icosidodécaèdre, dodéci 12 étoiles à 10 branches
Modèle assez facile à construire, 152 pièces, des grandes étoiles à 10 branches, qu'il vaut mieux renforcer, les pentagones sont parallèles aux étoiles, ce modèle n'est pas trop spectaculaire, ressemble trop à un dodécaèdre.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W81
Un W81 vu d'une face triangulaire
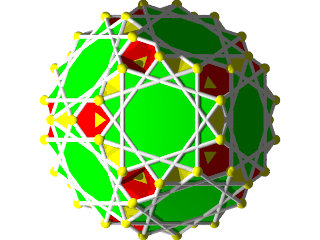
Un W81 vu d'une face en forme d'étoile à 10 branches
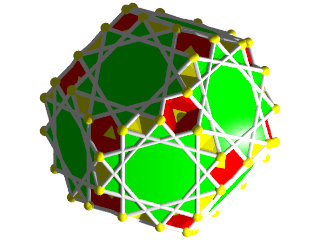
Un W81 vu d'un sommet
Le W81 et sa figure de sommet
la figure de sommet du W81, le grand côté pentagone, en face du petit côté étoile, relié par 2 triangles
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un dodécaèdre tronqué régulier
Il possède les mêmes sommets qu'un dodécaèdre tronqué régulier, qu'un W88 et qu'un W101
Il possède les mêmes arêtes qu'un W88, W101
Il possède les mêmes faces pentagonales et triangulaires qu'un W88
Il possède les mêmes faces en forme d'étoiles à 10 branches qu'un W101
Faces : 12{5}+12{10/3}+20{3}
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5 | 5/3
les étoiles à 10 branches {10/3} sont vues en entier
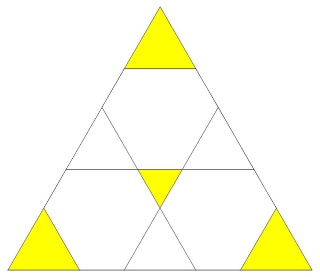
Alors que les triangles sont coupés
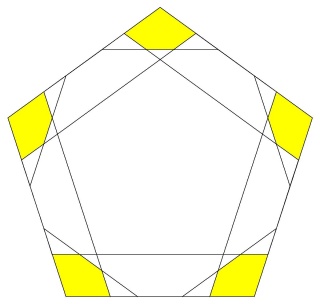
Ainsi que les pentagones
Rayon de la sphère circonscrite Racine de ((17-3 racine(5))/2) pour une arête de longueur 2 comme le W88 et le W101
Références :
p.125 de Polyhedron Models
p.109 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 54
W82
Petit dodecicosidodécaèdre ditrigonal ( Wikipédia )
12 décagones et 30 triangles comme un icosidodécaèdre et 12 pentagramme dodec...
Symétrie icosaédrique
Ce polyèdre avait échappé à l'analyse de Badoureau, Bruckner.... Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
212 pièces, la petite difficulté réside dans les cavités sous les pentagrammes. Les décagrammes sont vus dessous puis dessus, on peut simplifier le montage en emboitant ces morceaux de décagone.
un W82
Un W82 vu d'une face triangulaire
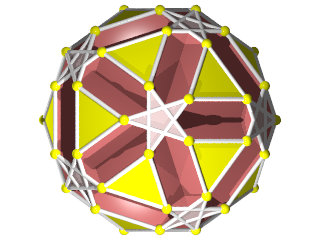
Un W82 vu d'une face pentagonale
un W82 vu d'un sommet
le W82 et sa figure de sommet
La figure de sommet du W82 un triangle en bas à gauche, un pentagramme en haut à droite et deux décagones qui se croisent.
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un petit rhombicosidodécaèdre irrégulier
Il possède les mêmes sommets que le W104 mais pas le même rayon circonscrit
Il possède les mêmes sommets que le W71 et le W90 avec le même rayon circonscrit
Il possède les mêmes arêtes que le W71 et le W90
Il possède les mêmes faces triangulaires et en forme de pentagrammes que le W71
Il possède les mêmes faces décagonales que le W90
Faces : 20{3}+12{10}+12{5/2}
Les pentagrammes sont vus en entier
ainsi que les triangles
alors que les décagones sont coupés et vus de dessus en jaune et de dessous en orange
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5/3 | 5
Rayon de la sphère circonscrite Racine de ((17+3 Racine(5)/2) pour une arête de longueur 2 comme le W71 et le W90
Références :
p.126-127 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 55
W83
Icosidodécadodécaèdre ( Wikipédia )
Symétrie icosaédrique
12 pentagones comme un dodécaèdre, 12 pentagrammes dodéca, 20 hexagones icosi
Ce modèle est assez spectaculaire avec ses 432 pièces. on peut tricher avec les hexagones qui sont vus dessus dessous, en emboîtant les pièces des hexagones on diminue le nombre de pièces à 186 en plus ce modèle est beaucoup plus facile à monter qu'il n'y paraît.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W83
Un W83 vu d'une face hexagonale
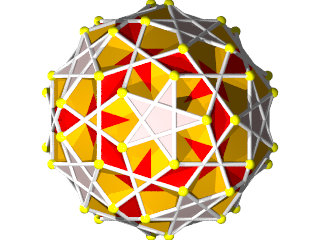
un W83 vu d'une face pentagonale
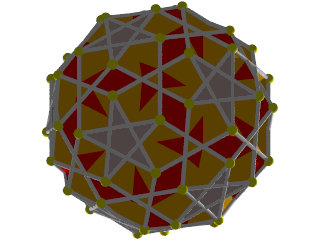
un W83 vu d'un sommet
Le W83 et sa figure de sommet
La figure de sommet du W83 un pentagramme en haut à droite un pentagone en bas à gauche et 2 hexagones en croix.
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier
Il possède les mêmes sommets qu'un W76 et qu'un W96
Il possède les mêmes arêtes qu'un W76 et qu'un W96
Il possède les mêmes faces pentagonales et en forme de pentagramme qu'un W76
Il possède les mêmes faces hexagonales qu'un W96
Faces : 20{6}+12{5}+12{5/2}
Les pentagrammes sont vus en entier
Mais pas les hexagones qui sont coupés et vus dessus en jaune et dessous en orange
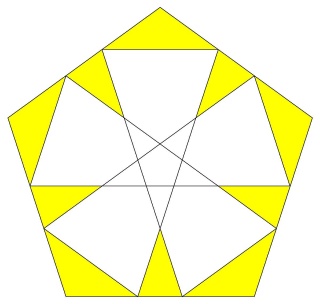
les pentagones sont également coupés
Sommets: 60
Arêtes : 120
Symbole de Wythoff 5/3 5 | 3
Rayon de la sphère circonscrite Racine de (7) pour une arête de longueur 2 comme le W76 et le W96
p.128-129 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 56
W84
Dodécadodécaèdre icositronqué ( Wikipédia )
symétrie icosaédrique
Un modèle facile à construire 152 pièces
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
un W84
un W84 vu d'une face hexagonale
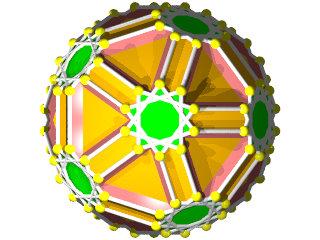
un W84 vu d'une face en forme d'étoile à 10 branches
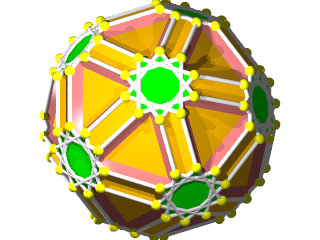
Un W84 vu d'un sommet
Le W84 et sa figure de sommet
La figure de sommet du W84 le grand côté le décagone, le petit l'étoile et le moyen l'hexagone
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un grand rhombicosidodécaèdre irrégulier
Faces : 20{6}+12{10}+12{10/3}
les étoiles à 10 branches sont vues en entier
alors que les hexagones sont coupés
ainsi que les décagones
Sommets: 120
Arêtes : 180
Symbole de Wythoff 3 5/3 5 |
Rayon de la sphère circonscrite 4 pour une arête de longueur 2
p.130-131 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 57
W85
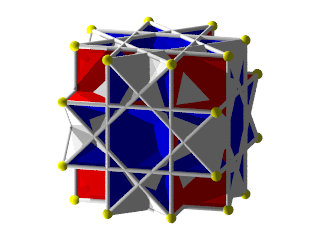
Grand rhombicuboctaèdre uniforme ( Wikipédia )
Symétrie octaédrique
8 triangles et 12+6 carrés comme un petit RhombiCubOctaèdre
Un modèle très spectaculaire et très difficile à réaliser avec 480 pièces, des cavités très profondes de nombreuses pièces à aligner, il me reste à le refaire en couleurs !
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Une petite photo de famille
Un W85
Un W85 vu d'une face carrée
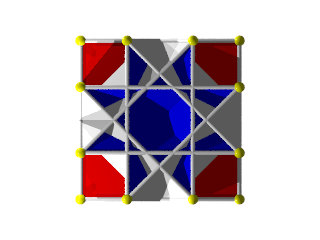
Un W85 vu d'une autre face carrée
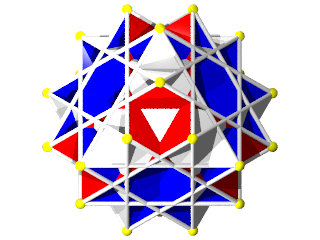
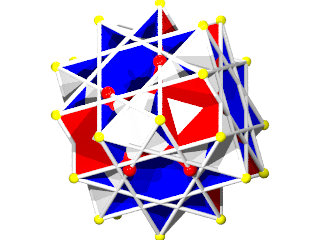
Un W85 vu d'une face triangulaire
Un W85 vu d'un sommet
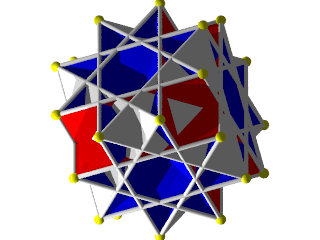
Un W85 et sa figure de sommet
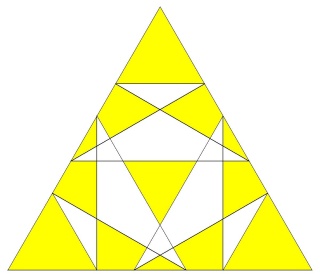
La figure de sommet d'un W85 seule
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un cube tronqué
Il possède les mêmes sommets qu'un cube tronqué, le W103 et le W77
Il possède les mêmes arêtes qu'un W77, W103
Il possède les mêmes faces carrées et triangulaires qu'un W77
Il possède les mêmes faces carrées qu'un W103
Faces : 8{3}+6{4}+12{4}
Les triangles sont coupés
les 6 carrés aussi
ainsi que le 12 carrés qui sont vus tantôt dessus en jaune, tantôt dessous en orange, remarquez que les deux sortes de carrés ne jouent pas le même rôle
Sommets: 24
Arêtes : 48
Symbole de Wythoff 3/2 4 | 2
Rayon de la sphère circonscrite Racine de (5-2Racine(2)) pour une arête de longueur 2 comme le W103 et le W77
p.132-133 de Polyhedron Models
p.99 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 59
W86
Petit Rhombihexaèdre ( Wikipédia )
Symétrie octaédrique
6 octogones dans les plans d'un cube d'où hexaèdre et 12 carrés donc un rhombi
66 pièces donc facile à faire mais très proche du rhombicuoctaèdre
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Une petite photo de famille
un W86
un W86 vu d'une face octogonale
un W86 vu d'une face carrée
un W86 vu d'un sommet
un W86 et sa figure de sommet
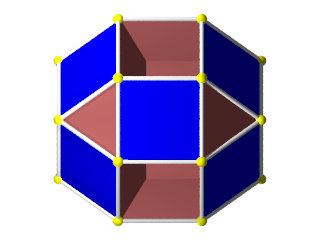
La figure de sommet d'un W86
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un petit rhombi-cuboctaèdre
Il possède les mêmes sommets qu'un petit rhombi-cuboctaèdre, qu'un W69 et qu'un W92.
Il possède les mêmes arêtes qu'un petit rhombi-cuboctaèdre
Il possède les mêmes faces carrées qu'un petit rhombi-cuboctaèdre
Il possède les mêmes faces octogonales qu'un W69
Faces : 12{4}+6{8}
Les carrés sont vus en entier
Alors que les octogones sont vus tantôt dessus en jaune et tantôt dessous en orange
Sommets: 24
Arêtes : 48
Symbole de Wythoff 2 4 | (3/2 4/2)
Rayon de la sphère circonscrite Racine de (5 + 2 Racine de deux) pour une arête de longueur 2 comme le W69 et le W92.
Références :
p.134 de Polyhedron Models
p.97 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 60
W87
Grand icosidodécaèdre ditrigonal ( Wikipédia )
Symétrie icosaédrique
12 pentagones et 20 triangles comme un icosidodécaèdre
Modèle fini le 28 octobre 2014, très spectaculaire, très coloré mais très difficile à réaliser, beaucoup de pièces, des creux très profonds, de très nombreux alignements à réaliser pour de beaux carrés....
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Un W87
Un W87 vu d'une face triangulaire
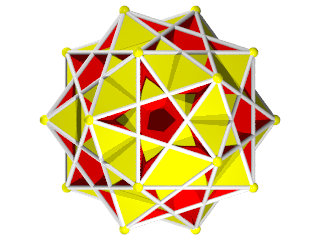
un W87 vu d'une face pentagonale
Un W87 vu d'un sommet
Un W87 et sa figure de sommet
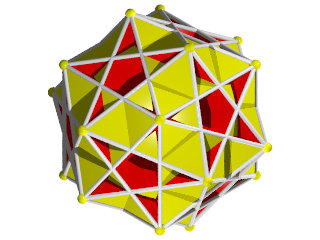
La figure de sommet d'un W87
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un dodécaèdre régulier.
Il possède les mêmes sommets qu'un dodécaèdre régulier.
Il possède les mêmes arêtes qu'un W70, W80 et que 5 cubes inscrits dans un dodécaèdre régulier.
Il possède les faces triangulaires qu'un W70.
Faces : 20{3}+12{5}
les triangles sont coupés,
les pentagones aussi.
Sommets: 20
Arêtes : 60
Symbole de Wythoff 3/2 | 3 5
Rayon de la sphère circonscrite Racine de 3 pour une arête de longueur 2 comme le W70 et le W80
Références :
p.135 de Polyhedron Models
p.98 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 61
W88
Grand icosicosidodécaèdre ( Wikipédia )
20 triangles et 12 pentagones comme un icosidodécaèdre et 20 hexagones icosi
Incroyable un W88 réalisé sur une imprimante 3D, j'ai réalisé le fichier Openscad et Olivier du fablab de Ris-Orangis Planète-Science l'a imprimé
C'est le premier polyèdre uniforme de la liste que je n'ai pas réalisé en papier! Il faut dire qu'avec ses 1232 pièces ce modèle est un défi pour les constructeurs de polyèdres ! Mais pas pour l'impression 3D
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Un W88
Un W88 vu d'une face triangle
un W88 vu d'une face pentagonale
Un W88 vu d'un sommet
Un W88 et sa figure de sommet
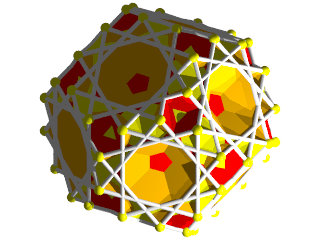
La figure de sommet d'un W88
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un dodécaèdre tronqué régulier
Il possède les mêmes sommets qu'un dodécaèdre tronqué régulier, W81, W101
Il possède les mêmes arêtes qu'un W81, W101
Il possède les mêmes faces pentagonales et triangulaires qu'un W81
Faces : 12{5}+20{6}+20{3}
les triangles sont très découpés,
ainsi que les pentagones,
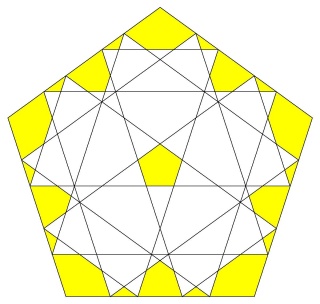
et que les hexagones tantôt vus dessus en jaune et dessous en orange.
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5 | 5/3
Rayon de la sphère circonscrite Racine de ((17-3 racine(5))/2) pour une arête de longueur 2
Références :
p.137-139 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 62
W89
Petit icosihémidodécaèdre ( Wikipédia)
Symétrie icosaédrique
20 triangles icosi Hémi la moitié des 12 décagones Dodéca
80 pièces donc en apparence ce modèle est facile à construire en fait les 6 décagones se pressant au centre rendent ce modèle délicat à réaliser.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Une photo de famille
un W89
un W89 vu d'une face triangle
un W89 vu d'une face décagonale.
un W89 vu d'un sommet
un W89 et sa figure de sommet
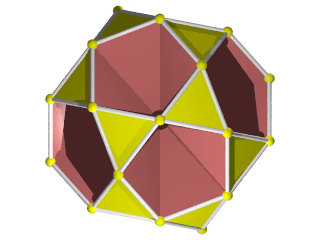
La figure de sommet du W89
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosidodécaèdre
Il possède les mêmes sommets qu'un icosidodécaèdre, W91
Il possède les mêmes arêtes qu'un W91, icosidodécaèdre
Il possède les mêmes faces décagonales qu'un W91
Faces : 6{10}+20{3}
les triangles sont vus en entier,
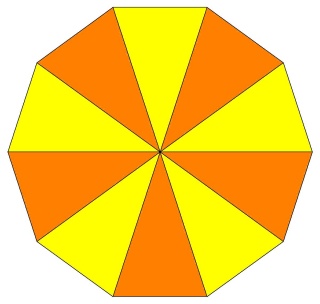
alors que les décagones équatoriaux sont vus, aussi en entier, mais tantôt dessus en jaune, tantôt dessous en orange.
Sommets: 30
Arêtes : 60
Symbole de Wythoff 3/2 3 | 5
Rayon de la sphère circonscrite 1+ Racine(5) pour une arête de longueur 2
Références :
p.140 de Polyhedron Models
p.96 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 63
W90
Petit dodécicosaèdre ( Wikipédia )
Symétrie icosaédrique
12 décagones dodéc 20 hexagones icosaèdre
Un modèle fini le 12/11/2014, très difficile 380 pièces, je l'ai fait assez gros mais pas encore assez car les pentagrammes étaient encore trop petits
Ce polyèdre avait échappé à l'analyse de Badoureau, Bruckner....comme le W82 que j'ai remis à droite. Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
Un W90
Un W90 vu d'une face hexagonale
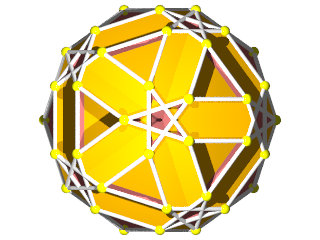
Un W90 vu d'une face décagonale
Un W90 vu d'un sommet
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un petit rhombicosidodécaèdre irrégulier
Il possède les mêmes sommets que le W104 mais pas avec le même rayon circonscrit
Il possède les mêmes sommets que le W71 et le W82 avec le même rayon circonscrit
Il possède les mêmes arêtes que le W71 et le W82
Il possède les mêmes faces hexagonales que le W82
Faces : 20{6}+12{10}
Les hexagones sont coupés,
ainsi que les décagones qui sont vus tantôt dessus en jaune et tantôt dessous en orange. ( Attention le schéma du décagone est partiellement faux dans Polyhedron Models )
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5 | (3/2 5/4)
Rayon de la sphère circonscrite Racine de ((17+3 Racine(5)/2) pour une arête de longueur 2 comme le W71 et le W82
p.141-142 de Polyhedron Models Attention le schéma du décagone est partiellement faux
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 64
W91
Petit dodécaHémiDodécaèdre ( Wikipédia )
Symétrie icosaédrique
12 pentagones dodéca Hémi la moitié de 12 Décagones HémiDodécaèdre
72 pièces mêmes remarques que pour le W89
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Un W91
Un W91 vu d'une face pentagonale
Un W91 vu d'un sommet
Un W91 et sa figure de sommet
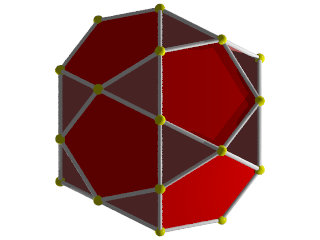
La figure de sommet du W91
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosidodécaèdre
Il possède les mêmes sommets qu'un icosidodécaèdre, W89
Il possède les mêmes arêtes qu'un W89, icosidodécaèdre
Il possède les mêmes faces décagonales qu'un W89
Faces : 6{10}+12{5}
les pentagones sont vus en entier,
alors que les décagones équatoriaux sont vus, aussi en entier, mais tantôt dessus en jaune, tantôt dessous en orange.
Sommets: 30
Arêtes : 60
Symbole de Wythoff 3/2 3 | 5
Rayon de la sphère circonscrite 1+ Racine(5) pour une arête de longueur 2
Références :
p.143 de Polyhedron Models
p.96 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 65
W92
W92 hexaèdre tronqué étoilé ( Wikipédia )
Symétrie octaédrique
Un charmant polyèdre, très facile à faire, 54 pièces.
Ce solide a été décrit la première fois par Albert Badoureau en 1881. Notez que son dessin est un peu faux.
Ce solide a été également et indépendamment décrit la première fois par J. Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900) Notez qu'il n'a pas non plus les bonnes proportions
Un W92
Un W92 vu d'une face en étoile à 8 branches
Un W92 vu d'une face triangulaire
Un W92 vu d'un sommet
Un W92 et sa figure de sommet
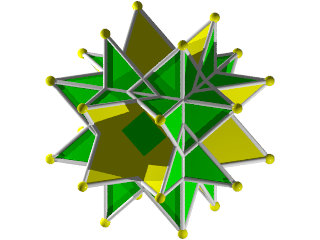
La figure de sommet d'un W92
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un petit rhombi-cuboctaèdre
Il possède les mêmes sommets qu'un petit rhombi-cuboctaèdre, qu'un et qu'un W69.
Faces : 8{3}+6{8/3}
les triangles sont coupés,
ainsi que les étoiles à 8 branches.
Sommets: 24
Arêtes : 48
Symbole de Wythoff 2 3 | 4/3
Rayon de la sphère circonscrite Racine de (7 + 4 Racine de deux) pour une arête de longueur 2
Références :
p.144 de Polyhedron Models
p.110 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 66
W93
Grand cuboctaèdre tronqué ( Wikipédia )
Symétrie octaédrique
Ce n'est pas que ce polyèdre soit compliqué 146 pièces mais sa structure interne complexe en fait un modèle pas très simple à construire pour un résultat final pas très spectaculaire.
Pour vous en convaincre quelques étapes de montage:
Ce solide a été décrit la première fois par Albert Badoureau en 1881. Notez que son dessin est un peu incomplet.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W93
Un W93 vu d'une face en forme d'étoile à 8 branches
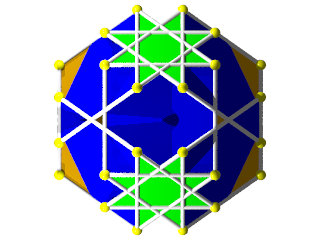
Un W93 vu d'une face carrée
Un W93 vu d'une face hexagonale
Un W93 vu d'un sommet
Un W93 et sa figure de sommet
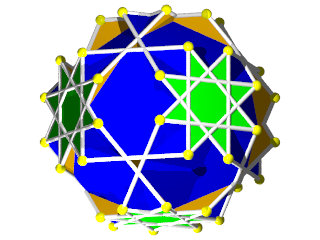
La figure de sommet d'un W93
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un grandt rhombi-cuboctaèdre non régulier
Faces : 8{6}+12{4}+6{8/3}
Les étoiles à 8 branches sont vues en entier.
alors que les carrés sont coupés.
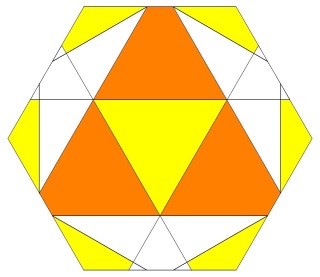
et les hexagones sont vus dessus en jaune et dessous en orange
Sommets: 48
Arêtes : 72
Symbole de Wythoff 2 3 4/3 |
Rayon de la sphère circonscrite Racine de (13 + 6 Racine de deux) pour une arête de longueur 2
Références :
p.145 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 67
W94
Grand icosidodécaèdre ( Wikipédia )
20 triangles et 12 pentagrammes
Symétrie Icosaédrique
Un modèle génial, pas trop compliqué 132 pièces et du plus bel effet avec ses étoiles à 10 branches équatoriales
Ce modèle est abondamment décrit dans la littérature.
C'est le seul polyèdre uniforme non convexe dont j'ai construit le dual qui lui est aussi abondamment décrit dans la littérature.
C'est même la couverture de Regular Polytopes, H.M.S. Coxeter, Dover
Ce solide a été décrit la première fois par Albert Badoureau en 1881. Notez que son dessin est un peu incomplet.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W94
Un W94 vu d'une face triangulaire
Un W94 vu d'une face en forme de pentagramme
un W94 vue d'un sommet
Un W94 et sa figure de sommet
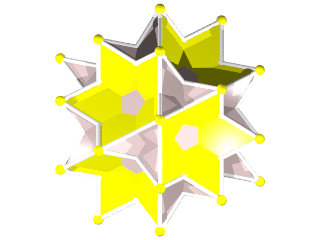
La figure de sommet du W94
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosidodécaèdre régulier
Il possède les mêmes sommets qu'un icosidodécaèdre, un W106, W107
Il possède les mêmes arêtes qu'un W106, W107
Il possède les mêmes pentagrammes qu'un W107
Il possède les mêmes triangles qu'un W106
Faces : 20{3}+12{5/2}
Les triangles sont coupés,
ainsi que les pentagrammes.
Sommets: 30
Arêtes : 60
Symbole de Wythoff 2 | 3 5/2
Rayon de la sphère circonscrite Racine de (5)-1 pour une arête de longueur 2.
Références :
p.147 de Polyhedron Models
p.115-117 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 70
p.124 de Mathematical Models, Cundy Rollett, Tarquin
p.101 de Regular Polytopes, H.M.S. Coxeter, Dover
Le Dual
p.103 de Regular Polytopes, H.M.S. Coxeter, Dover
p.126 de Mathematical Models, Cundy Rollett, Tarquin
p.117 de Shapes, Space and Symmetry, Alan Holden, Dover
W95
Grand icosaèdre tronqué ( Wikipédia )
Symétrie Icosaédrique
Modèle terminé le 01/11/2014, 192 pièces mais je l'ai construit beaucoup trop petit. J'ai longtemps été intrigué par les faux sommets qui forment des petites rosettes.
Ce solide a été décrit la première fois par J.Pitsch en 1881.
Un W95
Un W95 vu d'une face hexagonale
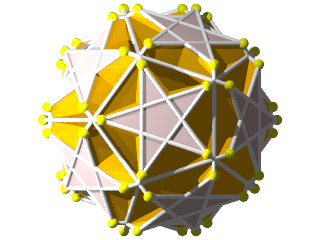
Un W95 vu d'une face en forme de pentagramme
un W95 vu d'un sommet
Un W95 et sa figure de sommet
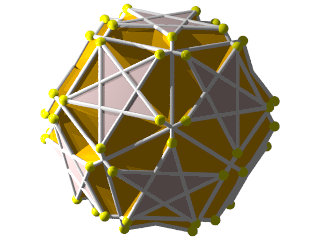
La figure de sommet d'un W95
ce polyèdre est inscrit dans un dodécaèdre tronqué irrégulier ou un Petit rhombicuboctaèdre irrégulier
Faces : 20{6}+12{5/2}
les pentagrammes sont vus en entier
alors que les hexagones sont coupés
Sommets: 60
Arêtes : 90
Symbole de Wythoff 2 5/2| 3
Rayon de la sphère circonscrite Racine de ((29-9Racine(5))/2)-pour une arête de longueur 2
Références :
p.148 de Polyhedron Models
p.104 de Shapes, Space and Symmetry, Alan Holden, Dover
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 71
W96
Rombicosaèdre ( Wikipédia )
Symétrie Icosaédrique
20 hexagones donc icosaèdre plus 30 carrés désigné par le terme Rhombi chez Kepler
Je n'ai pas construit ce modèle, mais 630 pièces, des cavités très profondes, de toutes petites pièces, des alignements, cela ne m'encourage pas ! (Enfin pas encore!)
Ce solide a été décrit la première fois par Albert Badoureau en 1881. Notez que son dessin est un peu incomplet.
Un W96
Un W96 vu d'une face hexagonale
Un W96 vu d'une face carrée
Un W96 vu d'un sommet
Un W96 et sa figure de sommet
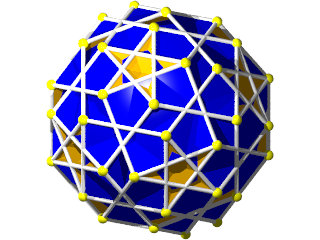
La figure de sommet d'un W96
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier
Il possède les mêmes sommets qu'un W83, W76
Il possède les mêmes arêtes qu'un W83, W76
Il possède les mêmes faces carrées qu'un W76
Il possède les mêmes faces hexagonales qu'un W83
Faces : 30{4}+20{6}
les carrés sont coupés
ainsi que les hexagones sont vus dessus en jaune et dessous en orange
Sommets: 60
Arêtes : 120
Symbole de Wythoff 2 3 | (5/4 5/2)
Rayon de la sphère circonscrite Racine de (7) pour une arête de longueur 2
p.149-150 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig. 72
W97
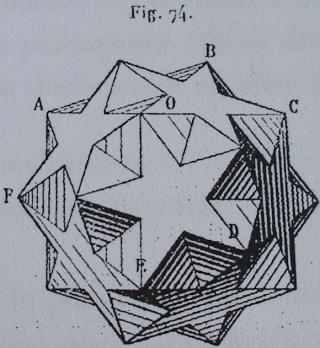
Petit dodécaèdre étoilé tronqué ( Wikipédia )
Symétrie Icosaédrique
Une troncature assez particulière du petit dodécaèdre étoilé (photo de droite)
132 pièces un polyèdre assez facile à réaliser
Ce solide a été décrit la première fois par Albert Badoureau en 1881. Notez la légère erreur de représentation des coupes pentagonales
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W97
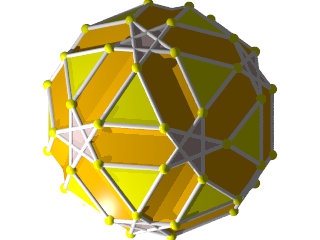
Un W97 vu d'une face en étoile à 10 branches
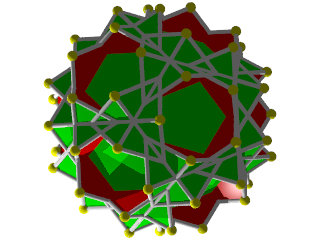
Un W97 vu d'un sommet
Un W97 et sa figure de sommet
La figure de sommet d'un W97
Quelques données sur ce polyèdre:
Ce polyèdre possède les mêmes sommets qu'un petit rhombicosidodécaèdre, W72
Faces : 12{5}+12{10/3}
les pentagones sont coupés
ainsi que les étoiles à 10 branches
Sommets: 60
Arêtes : 90
Symbole de Wythoff 2 5 | 5/3
Rayon de la sphère circonscrite Racine de ((17_5Racine(5))/2) pour une arête de longueur 2
p.151 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 74
p.111 de Shapes, Space and Symmetry, Alan Holden, Dover
W98
DodécaDodécaèdre tronqué ( Wikipédia )
Symétrie Icosaédrique
Comme vous le voyez je n'ai pas encore réalisé ce polyèdre de 402 pièces qui est le pendant icosaédrique du W93 octaédrique.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900) sous une forme légèrement différente
Un W98
Un W98 vu d'une face carrée
un W98 vu d'une face en forme d'étoile à 10 branches
Un W98 vu d'un sommet
Un W98 et sa figure de sommet
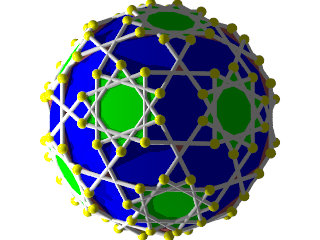
La figure de sommet du W98
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un grand rhombicosidodécaèdre irrégulier
Faces : 12{10}+30{4}+12{10/3}
les étoiles à 10 branches sont vues en entier
alors que les carrés sont coupés
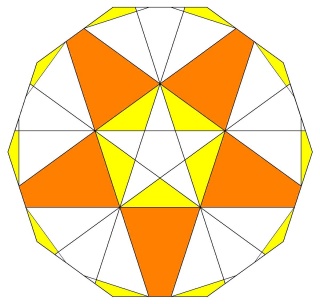
comme les décagones vus dessus en jaune et dessous en orange
Sommets : 120
Arêtes : 180
Symbole de Wythoff 2 5/3 5|
Rayon de la sphère circonscrite Racine de (11) pour une arête de longueur 2
p.152-153 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 75
W99
grand dodécicosidodécaèdre ( Wikipédia )
Symétrie Icosaédrique
12 pentagrammes Docec 20 triangles Icosi 12 étoiles à 10 branches Dodéca
Un polyèdre assez facile à construire 180 pièces et assez spectaculaire
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W99
Un W99 vu d'une face triangulaire
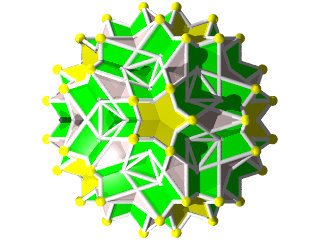
Un W99 vu d'une face en forme d'étoile à 10 branches
Un W99 vu d'un sommet
Un W99 et sa figure de sommet
La figure de sommet d'un W99
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier
Il possède les mêmes sommets qu'un W74, W99, W105
Il possède les mêmes arêtes que le W109 , W105
Il possède les mêmes faces en forme d'étoiles à 10 branches que le W109
Il possède les mêmes faces en forme de pentagrammes et de triangles que le W105
20{3}+12{5/2}+12{10/3}
les étoiles à 10 branches sont coupées
ainsi que les pentagrammes,
et les triangles
Rayon de la sphère circonscrite Racine(11 - racine(5)) pour une arête de longueur 2
p.154 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig. 77
W100
Petit Dodécahémicosaèdre ( Wikipédia )
Symétrie Icosaédrique
12 pentagrammes dodéca et la moitié des 20 hexagones (ils sont équatoriaux)
Malgré son faible nombre de pièces 132 ce polyèdre est une galère à construire, un centre très encombré par les 10 hexagones équatoriaux, des morceaux qui tiennent par des arêtes en plus je l'ai fait trop petit.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W100
Un W100 vu d'une face hexagonale
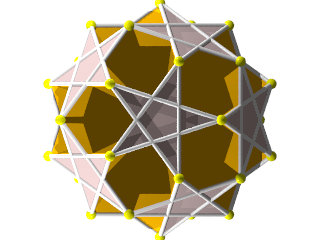
Un W100 vu d'une face en forme de pentagramme
Un W100 vu d'un sommet
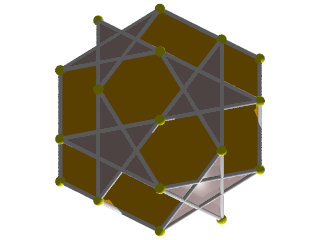
Un W100 et sa figure de sommet
La figure de sommet d'un W100
Quelques données sur ce polyèdre:
Ce polyèdre est inscrit dans un icosidodécaèdre
Il possède les mêmes sommets qu'un W73, W102
Il possède les mêmes arêtes qu'un W73, W102
Faces : 10{6}+12{5/2}
Sommets: 30
Arêtes : 60
Symbole de Wythoff 5/3 5/2 | 3
Les pentagrammes sont vus en entier
alors que les hexagones équatoriaux sont tantôt vus dessus en jaune, tantôt vus dessous en orange.
Rayon de la sphère circonscrite 2 pour une arête de longueur 2 comme le W73 et le W102
p.155 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 78
W101
Grand dodécicosaèdre ( Wikipédia )
Symétrie Icosaédrique
12 étoiles à 10 branches dodec 20 hexagones icosaèdre
Je n'ai pas construit ce modèle de 362 pièces
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Un W101 vu d'une face hexagonale
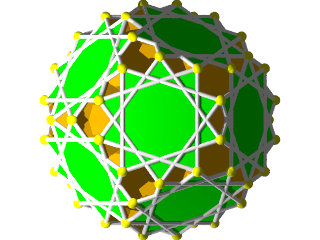
Un W101 vu d'une face en forme d'étoile à 10 branches
Un W101 vu d'un sommet
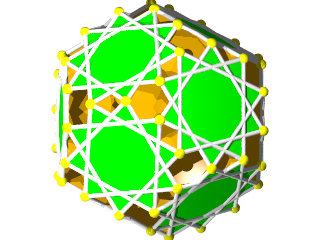
Un W101 et sa figure de sommet
La figure de sommet du W101 seule
Quelques données sur ce polyèdre:
ce polyèdre est inscrit dans un dodécaèdre tronqué régulier
Il possède les mêmes sommets qu'un dodécaèdre tronqué régulier, W88, W811
Il possède les mêmes arêtes qu'un W88, W811
Il possède les mêmes faces hexagonales qu'un W88
Il possède les mêmes faces en forme d'étoiles à 10 branches qu'un W81
Faces : 20{6}+12{10/3}
les étoiles à 10 branches sont vues en entier,
alors que les hexagones sont coupés et vus tantôt dessus en jaune, tantôt dessous en orange.
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5 | 5/3
Rayon de la sphère circonscrite Racine de ((17-3 racine(5))/2) pour une arête de longueur 2
Références :
p.156-157 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 79
W102
Grand dodécaHémIcosaèdre ( Wikipédia )
Symétrie Icosaédrique
12 pentagones Dodéca HémIcosaèdre La moitié des 20 Hexagones
Modèle fini le 29 août 2014, 312 pièces, modèle assez difficile à réaliser car les cavités sont très profondes
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W102
un W102 vu d'une face hexagonale
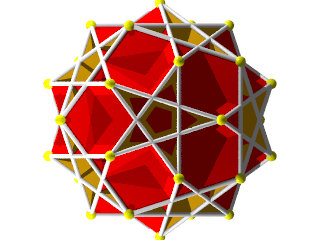
un W102 vu d'une face pentagonale
un W102 vu d'un sommet
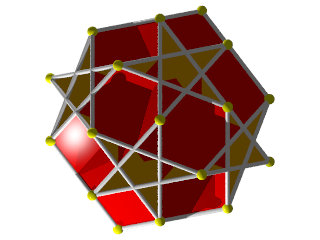
Un W102 et sa figure de sommet
la figure de sommet seule, les traits verticaux sur les pentagones et les traits croisés sur les hexagones
Ce polyèdre est inscrit dans un icosidodécaèdre
Il possède les mêmes sommets qu'un W73, W100
Il possède les mêmes arêtes qu'un W73, W100
Il possède les mêmes hexagones qu'un W100
Il possède les mêmes pentagones qu'un W73
Faces : 10{6}+12{5}
les pentagones sont coupés
les hexagones aussi, tantôt vus dessus en jaune ou dessous en orange
Sommets: 30
Arêtes : 60
Symbole de Wythoff 5/4 5 | 3
Rayon de la sphère circonscrite 2 pour une arête de longueur 2 comme le W73 et le W100
p.158 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 81
W103
Le grand rhombiHexaèdre ( Wikipédia )
Symétrie Octaédrique
12 carrés comme les rhombi et 6 étoiles à 8 branches 6 = hexa
Un polyèdre assez facile à construire avec ses 126 pièces, les cavités sont très profondes, mais assez larges.
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W103
un W103 vu des étoiles à 8 branches
un W103 vu des carrés
un W103 vu d'un sommet
un W103 et sa figure de sommet
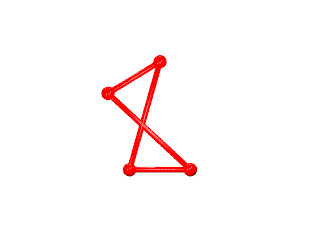
la figure de sommet seule du W103
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un cube tronqué
Il possède les mêmes sommets qu'un cube tronqué, W77, W85
Il possède les mêmes arêtes qu'un W85, W77
Il possède les mêmes faces carrées qu'un W85
Il possède les mêmes faces en forme d'étoile à 8 branches qu'un W77
Faces : 12{4}+6{8/3}
Les étoiles à 8 branches sont vues en entier
alors que les carrés sont coupés et vus dessus en jaune et dessous en orange.
Sommets: 24
Arêtes : 48
Symbole de Wythoff 3 4 | 4/3
Rayon de la sphère circonscrite Racine de (5-2Racine(2)) pour une arête de longueur 2
p.159-160 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 82
W104
Le grand dodécaèdre étoilé quasitronqué ( Wikipédia )
Symétrie Icosaédrique
C'est un grand dodécaèdre étoilé dont on aurait savamment tronqué les pointes d'où le quasi tronqué
Un modèle spectaculaire et très facile à faire puisque qu'il suffit d'assembler 20 coupes de 6 pièces soit 120 pièces
Ce solide a été décrit la première fois par J.Pitsch en 1881
on trouve ce solide dans le livre de Max Brückner Vielecke-Und-Vielflache, (1900)
Un W104
Un W104 vu d'une face triangulaire
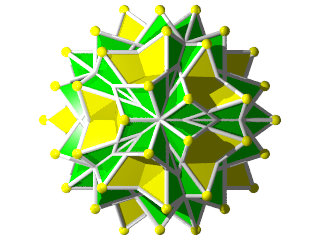
un W104 vue d'une face en forme d'étoile à 10 branches
Un W104 vu d'un sommet
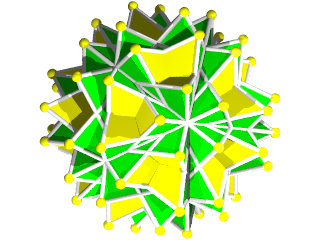
Un W104 et sa figure de sommet
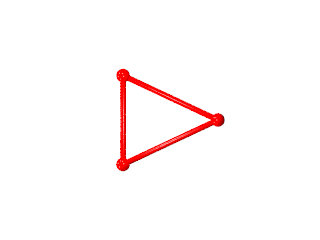
La figure de sommet du W104 seule un triangle isocèle les deux grands côtés sut l'étoile à 10 branches et le petit côté sur le triangle
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un petit rhombicosidodécaèdre irrégulier
Il possède les mêmes sommets qu'un W71, W82, W90 mais pas le même rayon circonscrit
Il possède les mêmes sommets qu'un W95 avec le même rayon circonscrit
Faces : 12{10/3}+20{3}
L'étoile à 10 branches est coupée
Les triangles aussi
Sommets: 60
Arêtes : 90
Symbole de Wythoff 3 5 | 5/3
Rayon de la sphère circonscrite Racine de ((37-15 Racine(5))/2) pour une arête de longueur 2
p.161 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 83
W105
QuasiRhombicosidodécaèdre ( Wikipédia )
Symétrie Icosaédrique
20 triangles Icosi 12 pentagrammes dodécaèdre + 30 carrés rhombi mais ce n'est pas le rhombicosidodécaèdre d'où quasi
Je n'ai pas (encore) construit ce modèle de 980 pièces !
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W105
un W105 vu d'une face triangulaire
un W105 vu d'une face carrée
un W105 vu d'un pentagramme
un W105 vu d'un sommet
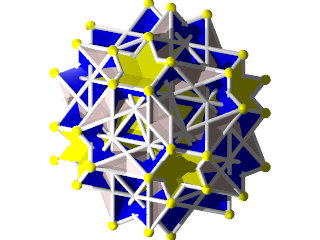
un W105 et sa figure de sommet
La figure de sommet seule du W105 le grand côté en haut à gauche est le triangle, le pentagramme en bas à droite et les deux carrés se croisent
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier
Il possède les mêmes sommets qu'un W75, W99, W109
Il possède les mêmes arêtes que le W99, W109
Il possède les mêmes pentagrammes et triangles que le W99
il possède les mêmes carrés que le W109
Faces : 30{4}+12{5/2}+20{3}
les pentagrammes sont coupés
les triangles aussi
les carrés également mais ils sont vus tantôt dessus en jaune, tantôt dessous en orange
Sommets: 60
Arêtes : 120
Symbole de Wythoff 3 5/2 | 2
Rayon de la sphère circonscrite Racine de (11-4Racine(5))) pour une arête de longueur 2
p.162-163 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 84
W106
Grand IcosiHémidodécaèdre ( Wikipédia )
Symétrie Icosaédrique
20 triangles Icosi 6 des 12 étoiles à 10 branches Hémi (moitié) dodécaèdre
180 pièces, pas trop difficile malgré les étoiles équatoriales et les cavités très profondes j'ai fini ce modèle le 22 octobre 2014
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W106
un W106 vu d'un triangle
Un W106 vu d'une étoile équatoriale à 10 branches
un W106 vu d'un sommet
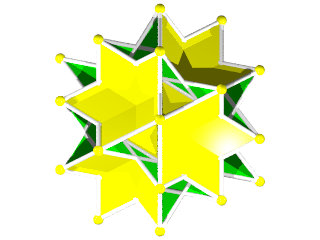
un W106 et sa figure de sommet
la figure de sommet du W106 seule les deux étoiles se croisent au centre, les deux triangles opposés
Quelques données sur ce polyèdre
ce polyèdre est inscrit dans un icosidodécaèdre.
Il possède les mêmes sommets qu'un icosidodécaèdre, W89, W91, W73, W100, W102, W107, W94.
Il possède les mêmes arêtes que le W107, W94.
Il possède les mêmes triangles que le W94.
Il possède les mêmes étoiles à 10 branches que le W107.
Faces : 6 {10/3} + 20 {3}
Les triangles sont coupés,
les étoiles à 10 branches aussi, vu de dessus en jaune, et dessous en orange.
Sommets: 30
Arêtes : 60
Symbole de Wythoff 3/2 3 | 5/3
Rayon de la sphère circonscrite Racine de (5)-1 pour une arête de longueur 2
p.164 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 85
p.114 de Shapes, Space and Symmetry, Alan Holden, Dover
W107
Grand dodécaHémiDodécaèdre ( Wikipédia )
Symétrie Icosaédrique
12 pentagrammes Dodéca 6 des 12 étoiles à 10 branches Hémi (moitié) dodécaèdre
Un modèle assez facile à faire avec 132 pièces, remarquez qu'il n'est constitué que d'étoiles (Pentagrammes et Décagrammes)
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W107
Un W107 vu d'une face
un W107 vu d'un sommet
Un W107 et sa figure de sommet
La figure de sommet du W107 seul, les grands côtés se croisent sur les étoiles à 10 branches, les petits côtés opposés sont sur les pentagrammes.
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un icosidodécaèdre
Il possède les mêmes sommets qu'un icosidodécaèdre, W89, W91, W102, W100, W102, W106, W94
Il possède les mêmes arêtes que le W106, W94
Il possède les mêmes pentagrammes que le W94
il possède les mêmes étoiles à 10 branches que le W106
Faces : 6{10/3}+12{5/2}
Sommets : 30
Arêtes : 60
Symbole de Wythoff 5/3 5/2 | 5/3
les pentagrammes sont coupés
les étoiles à 10 branches aussi, vu de dessus en jaune, et dessous en orange
Rayon de la sphère circonscrite Racine de (5)-1 pour une arête de longueur 2
p.165 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 86
p.115 de Shapes, Space and Symmetry, Alan Holden, Dover
W108
grand icosidodécaèdre tronqué ( Wikipédia )
Symétrie Icosaédrique
Ce polyèdre incroyablement complexe a été réalisé sur une imprimante 3D
le 05 septembre 2015, 7 cm de hauteur
(Toujours réalisé par Olivier au fab lab de Ris Orangis Planète Science, la conception du fichier OpenScad réalisée par Jean-Jacques Dupas)
Je n'ai pas (encore) réalisé ce polyèdre extrêmement complexe de 1020 pièces en papier
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
Ce solide a été également et indépendamment décrit la première fois par J.Pitsch en 1881
un W108
un W108 vu d'une face hexagonale
un W108 vu d'une face carrée
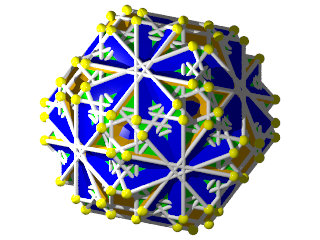
un W108 vu d'une face en forme d'étoile à 10 branches
un W108 vu d'un sommet
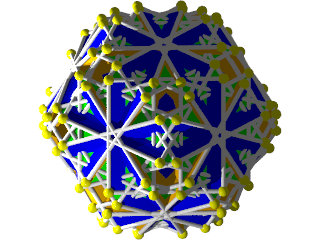
un W108 et sa figure de sommet
La figure de sommet du W108 seule, le grand côté sur un hexagone, le moyen sur une étoile à 10 branches et le petit côté sur un carré.
Quelques données sur ce polyèdre :
Ce polyèdre est inscrit dans un grand rhombicosidodécaèdre irrégulier
Faces : 12{10/3}+20{6}+30{4}
les carrés sont coupés,
les hexagones aussi,
ainsi que les étoiles à 10 branches.
Sommets: 120
Arêtes : 180
Symbole de Wythoff 2 3 5/3 |
Rayon de la sphère circonscrite Racine de (11-4Racine(5)) pour une arête de longueur 2
p.166-167 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 87
W109
Grand RhombiDodécaèdre ( Wikipédia )
Symétrie Icosaédrique
12 étoiles à 10 branches Dodécaèdre, 30 carrés le rhombi
Je n'ai pas (encore) construit ce polyèdre complexe de 612 pièces
Ce solide a été décrit la première fois par Albert Badoureau en 1881.
un W109
Un W109 vu d'une face carrée
un W109 vu d'une face en forme d'étoile à 10 branches
un W109 vu d'un sommet
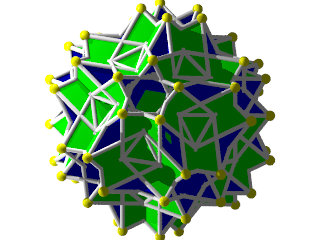
un W109 et sa figure de sommet
La figure de sommet du W109 seul, les côtés sur les carrés se croisent au milieu reliant les côtés sur les étoiles à 10 branches
Quelques données sur ce polyèdre
Ce polyèdre est inscrit dans un icosaèdre tronqué irrégulier.
Il possède les mêmes sommets qu'un W74, W99, W105.
Il possède les mêmes arêtes que le W99, W105 que le W99
Il possède les mêmes carrés que le W105
Il possède les mêmes étoiles à 10 branches que le W99
Faces : 30{4}+12{10/3}
Les étoiles à 10 branches sont coupées,
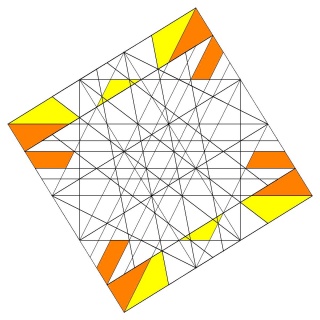
ainsi que les carrés vus s dessus en jaune et dessous en orange.
Sommets: 60
Arêtes : 120
Symbole de Wythoff 2 5/3(3/2 5/4) |
Rayon de la sphère circonscrite Racine de (11-4Racine(5))) pour une arête de longueur 2
p.168-169 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 89
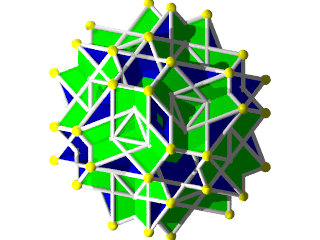
W110
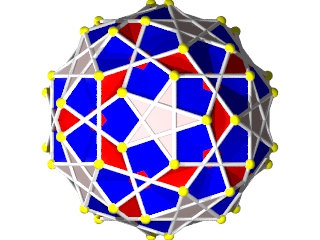
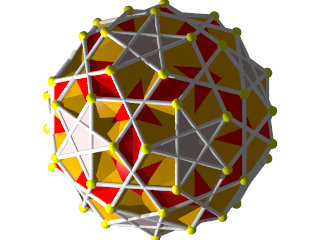
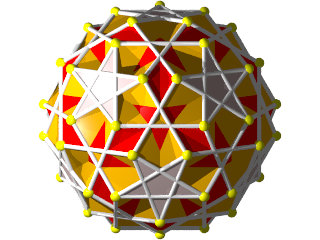
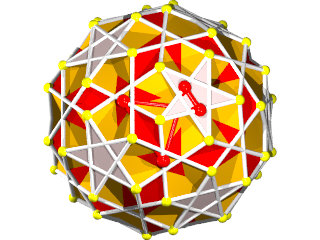
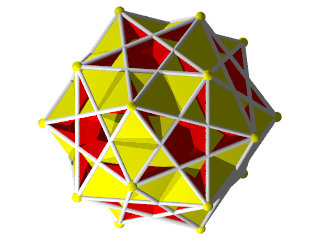
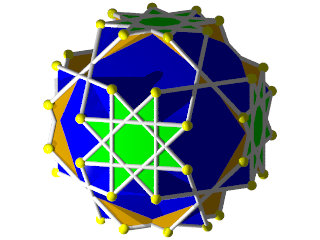
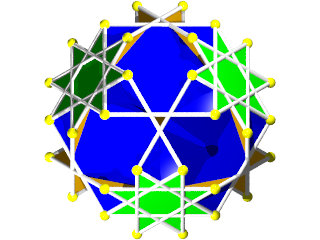
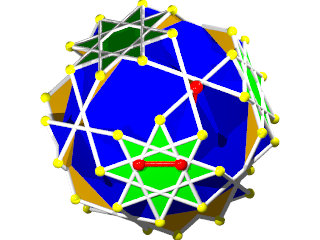
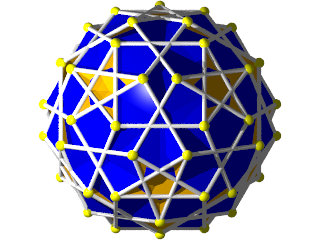
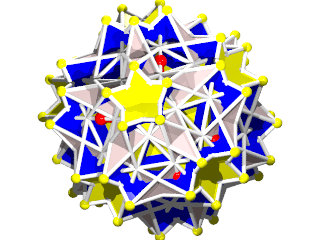
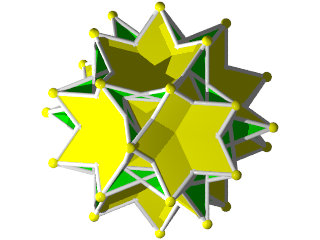
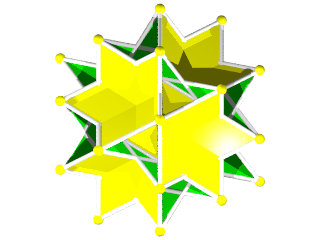
Petit IcosIcosiDodécaèdre Camus ( Wikipédia )
Construit le 11 mai 2015
Symétrie Icosaédrique
Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
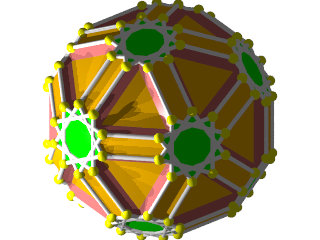
Un polyèdre camus très coloré, 5 couleurs pour les triangles et 1 pour les pentagrammes, facile à construire (212 pièces) mais difficile à calculer, c'est un polyèdre camus avec plans de symétrie, Albert Badoureau aurait pu le découvrir, j'explique pourquoi plus bas
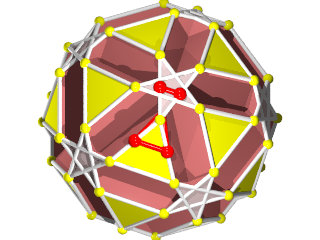
12 pentagrammes (Suivant les axes des pentagones du dodécaèdre)
40 triangles (2x20 suivant les axes des triangles de l'icosaèdre )
60 triangles (presque dans l'axe des sommets)
La méthode pour calculer le W110 et le W118 est une adaptation de la méthode de Badoureau, elle est à ma connaissance nouvelle et publiée ici pour la première fois, elle m'a permis d'obtenir ces deux polyèdres assez facilement, quelques heures avec le secours du calcul formel.
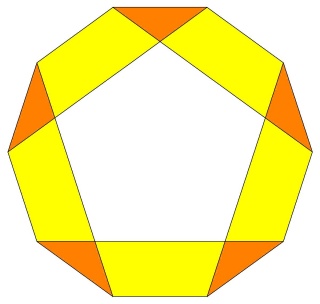
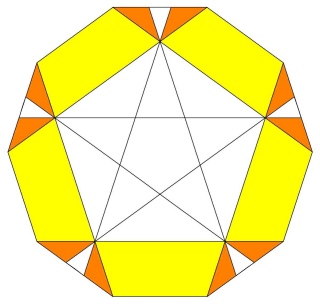
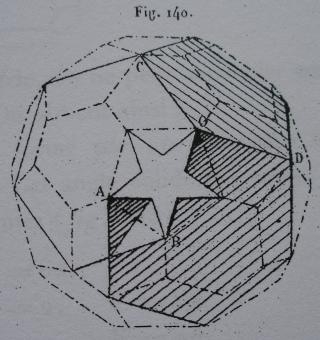
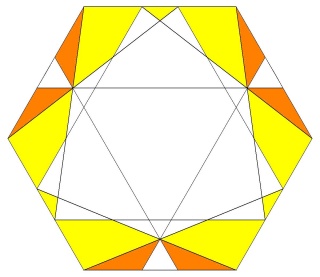
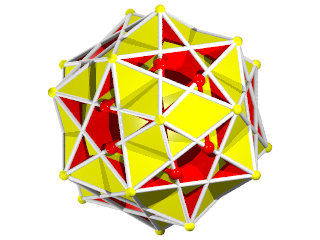
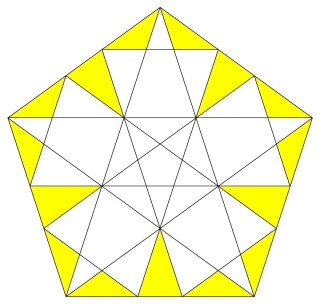
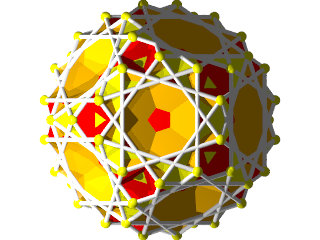
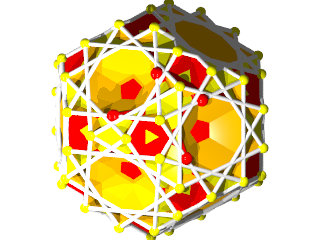
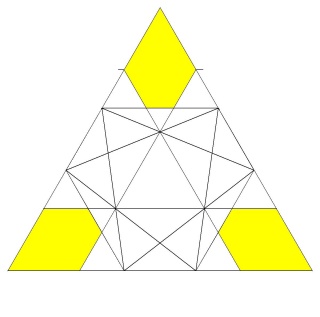
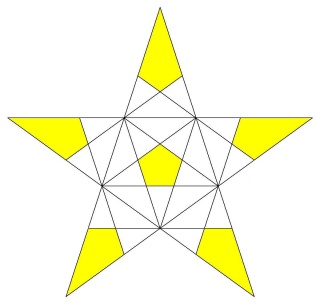
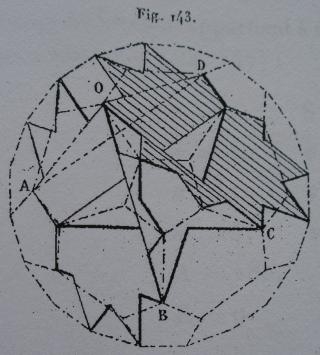
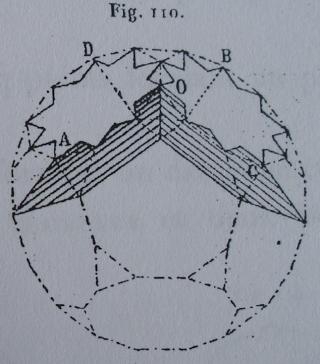
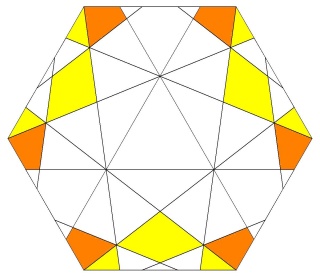
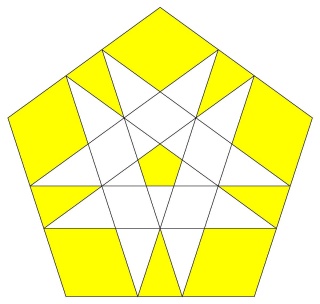
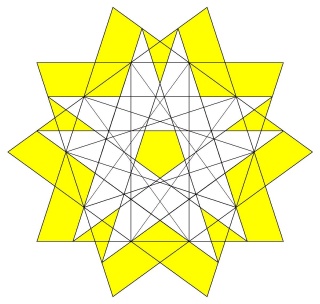
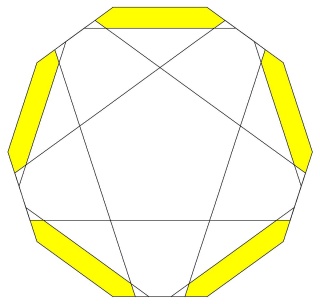
Une des idées géniales de Badoureau est de considérer des polyèdres archimédiens modifiés comme un icosaèdre tronqué dont les pentagones sont toujours réguliers et dont la longueur d'un côté sur deux des hexagones est réglable (ci-dessous l'enveloppe convexe du W110)
d'un point de vue calculatoire on part d'un icosaèdre, et sur chaque arête on définit deux nouveaux points qui sont à une distance lambda de chaque sommet, mais vers l'autre sommet. Le polyèdre sur lequel on travaille est l'enveloppe convexe de nos nouveaux points, par construction ils sont 60 soit deux fois plus que les arêtes de l'icosaèdre.
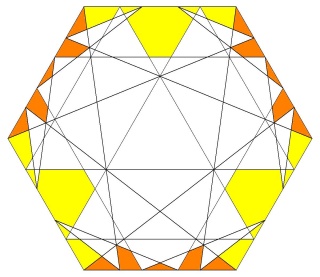
Dans ce cadre il n'est pas possible d'avoir la longueur des arêtes du pentagramme égale aux arêtes des hexagones.
Mais Badoureau a oublié que l'on pouvait séparer les hexagones en 2 triangles en prenant un sommet sur deux de chaque hexagone. Nous obtenons une équation en lambda qui admet deux solutions, une positive qui nous permet de continuer le calcul, une négative qui donne le W118.
Maintenant il ne reste plus qu'à remarquer que l'on peut reboucher les trous avec 60 triangles supplémentaires presque dans l'axe des sommets et cela nous donne ce polyèdre camus, ces calculs étaient largement à la portée de Badoureau qui à conduit des calculs bien plus complexes et brillants.
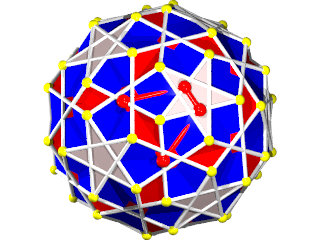
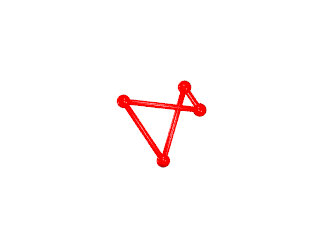
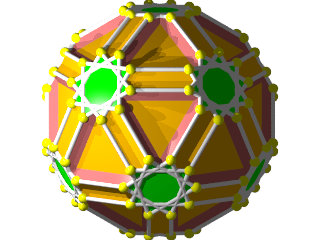
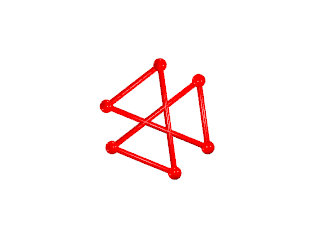
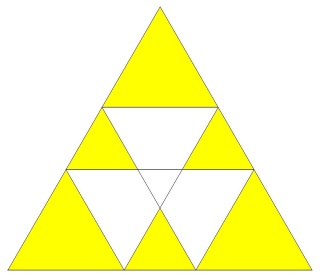
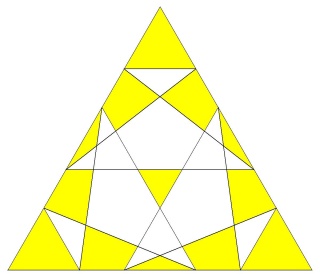
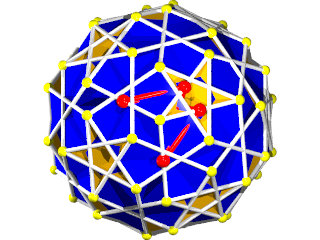
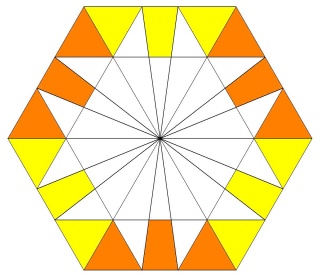
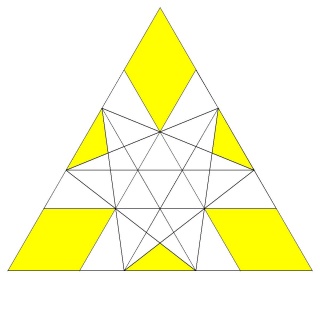
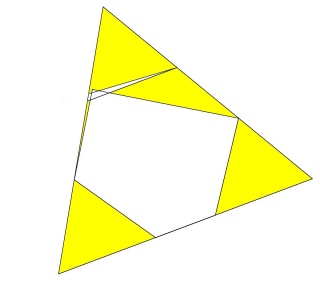
Ce polyèdre est camus car si les pentagrammes sont bien les pentagrammes habituels des polyèdres réflexifs les triangles auraient dû être dans la configuration de l'image suivante :
Les triangles bleus ont été dédoublés et tournés pour venir sur les sommets des pentagrammes, ce qui dans ce cas donne l'aspect camus, notez que les deux triangles font un angle de presque 30° (27°64) donc les triangles qui apparaissent par paires ne forment pas une étoile de David.
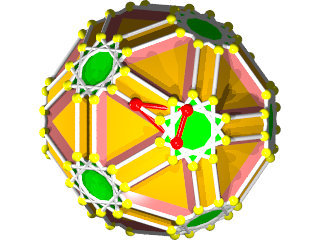
La première étape de la construction
Quelques données sur ce polyèdre
Faces : (40+60) {3}+12 {5/2}
les 12 pentagrammes sont vus en entier
Les 40 triangles aussi mais ils sont entrelacés
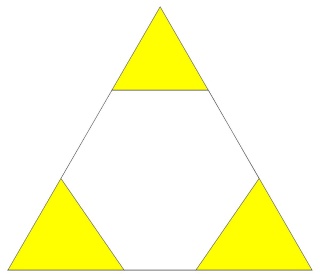
Par contre les 60 triangles sont coupés
60 sommets
Symbole de Wythoff | 3 3 5/2
Rayon de la sphère circonscrite 1/2 Racine de ( 13 + 3 Racine(5) +Racine(102+46 Racine(5))) pour une arête de longueur 2
C'est à ma connaissance la première fois que l'on donne une expression exacte de ce rayon, un peu complexe j'en conviens, soit 2.916380661477405102
p.172-173 de Polyhedron Models
Il a été publié la première fois en 1954 dans l'articleCoxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 41
W111
dodécadodécaèdre camus ( Wikipédia )
Symétrie Icosaédrique
60{3}+12{5/2}+12{5}
Le diagramme des 60 triangles. Notez les minuscules échardes qui font le charme de ce polyèdre
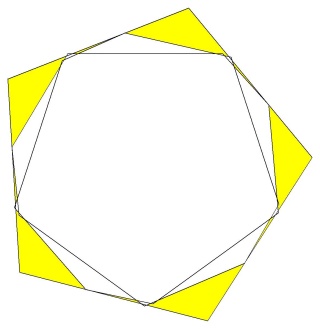
Le diagramme des 12 pentagones notez, encore une fois, les minuscules échardes qui font le charme de ce polyèdre
les 12 pentagramme sont vus en entier
60 sommets (inscrit dans un dodécaèdre camus modifié)
Il a été décrit pour la première fois par Lesavre & Mercier, sans dessin, en 1947
p.174-176 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 49
W112
IcosiDodécaDodécaèdre Camus ( Wikipédia)
Symétrie Icosaédrique
Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 58
p.177-178 de Polyhedron Models
W113
grand icosidodécaèdre camus inversé ( Wikipédia )
Symétrie Icosaédrique
Il a été décrit pour la première fois par Lesavre & Mercier, sans dessin, en 1947
Voici un très beau modèle réalisé le 24 janvier 2016 au fab-lab de Ris-Orangis
Voici matérialisé un pentagramme
et ci-dessous 2 triangles
à chaque sommet 4 triangles et un pentagramme : un modèle délicieux avec ses rosettes pentagonales
p.179 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 73
W114
DodécaDodécaèdre camus inversé ( Wikipédia )
Symétrie Icosaédrique
Il a été décrit pour la première fois par Lesavre & Mercier, sans dessin, en 1947
p.180-182 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 76
W115
Grand DodécIcosiDodécaèdre Camus ( Wikipédia )
Symétrie Icosaédrique
Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
(20+60) {3} +(12+12) {5/2}
Le diagramme des 20 triangles
Le diagramme des 60 triangles
Le diagramme des deux pentagrammes coplanaires
Rayon de la sphère circonscrite Racine de (2) pour une arête de longueur 2
Cp.183-185 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 80
W116
Grand IcosiDodécaèdre Camus ( Wikipédia )
Symétrie Icosaédrique
Il a été décrit pour la première fois par Lesavre & Mercier, sans dessin, en 1947
p.186-188 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 88
W117
Grand icosidodécaèdre rétroCamus ( Wikipédia )
Symétrie Icosaédrique
Il a été décrit pour la première fois par Lesavre & Mercier, sans dessin, en 1947
p.189-193 de Polyhedron Models
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 90
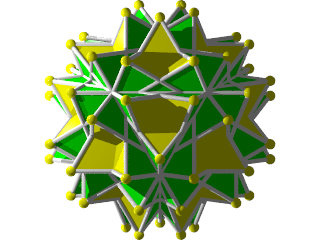
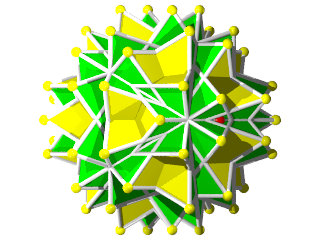
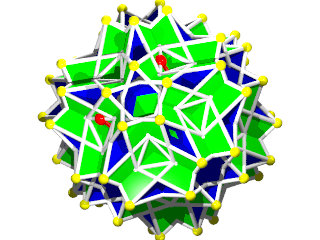
W118
Petit IcosIcosiDodécaèdre rétroCamus ( Wikipédia )
Symétrie Icosaédrique
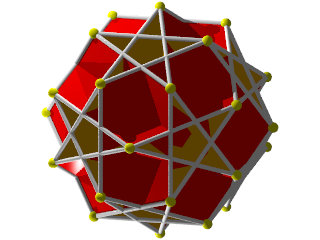
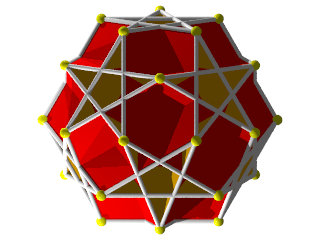
De plus en plus fort! Un W118 imprimé sur une imprimante 3D début juillet 2015, 9 cm de hauteur
un deuxième réalisé le 03 septembre 2015, 13 cm de hauteur
(Toujours réalisé par Olivier au fab lab de Ris Orangis Planète Science, la conception du fichier OpenScad réalisée par Jean-Jacques Dupas)
les deux ensembles
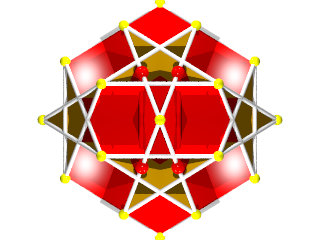
Le W118 peut être obtenu comme le W110
Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
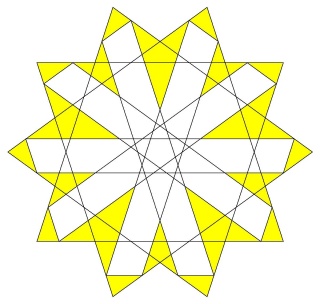
Voici les pentagrammes de la deuxième solution (Attention il y en a un blanc au premier plan un peu trop éclairé) nous voyons que les pentagrammes s'enchevêtrent, le fait de trouver une solution négative veut dire que les nouveaux sommets sont au delà de l'icosaèdre ce qui provoque l'enchevêtrement des pentagrammes
Puis on ajoute les 20 triangles dédoublés soit 40 triangles enchevêtrés
Pour finir on ajoute les 60 triangles rouges pour refermer le polyèdre
Là il est beaucoup moins facile de voir où ajouter les 60 triangles rouges de la première figure
Même si en théorie ce polyèdre était accessible par Badoureau, les calculs ne sont pas plus compliqués que pour le W110 c'est moins simple en pratique, puisque même avec l'objet réel sous les yeux difficile de s'y retrouver.
Ce polyèdre camus possède des plans de symétrie et 1630 pièces si on veut le construire, une paille!
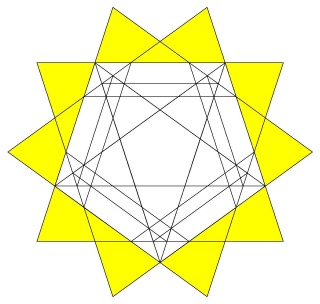
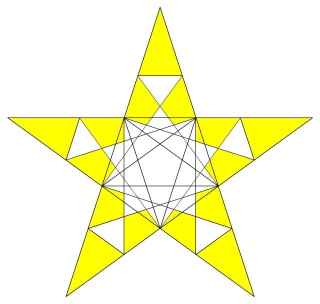
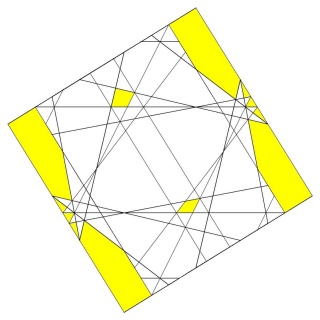
Pour se convaincre de la complexité de ce polyèdre voici sur la figure suivante une face en forme de pentagramme coupée par toutes les autres faces
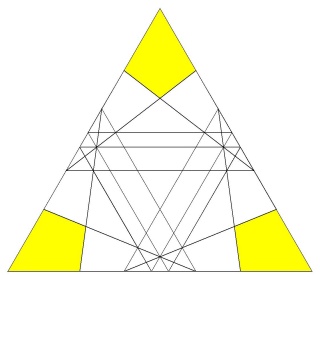
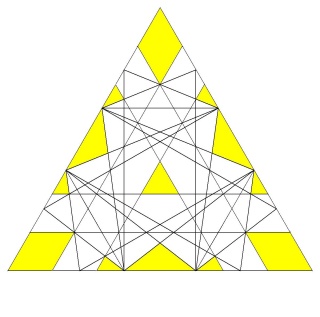
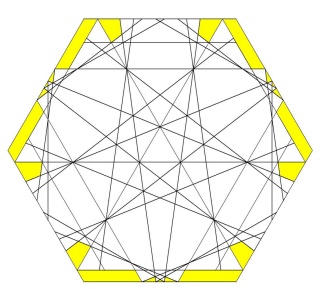
Puis les deux triangles coplanaires (Ce sont les 40 triangles qui apparaissent par paires) coupés par les autres faces
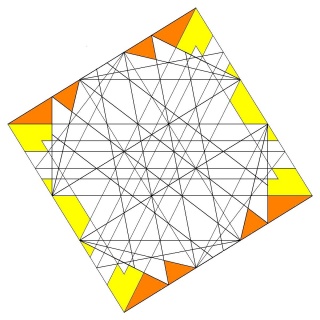
Enfin la dernière sorte triangle (les 60 triangles) coupée par les autres faces
Quelques données sur ce polyèdre
(40+60) {3}+12 {5/2}
60 sommets
Symbole de Wythoff | 3/2 3/2 5/2
Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 91
p.194-199 de Polyhedron Models
W119
Grand DiRhombIcosiDodécaèdre ( Wikipédia )
Symétrie Icosaédrique
(20+20){3}+(30+30){4}+(12+12){5/2}
Les 2 fois 12 pentagrammes coplanaires coupés
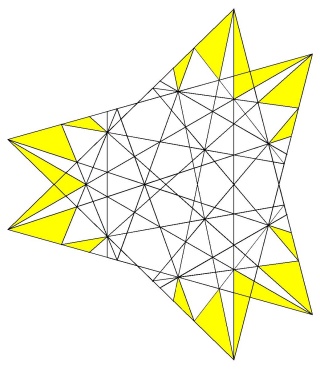
les 2 fois 20 triangles coplanaires coupés
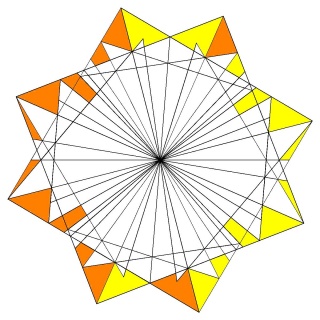
les 2 fois 30 carrés coplanaires coupés et vus de dessus en jaune et de dessous en orange
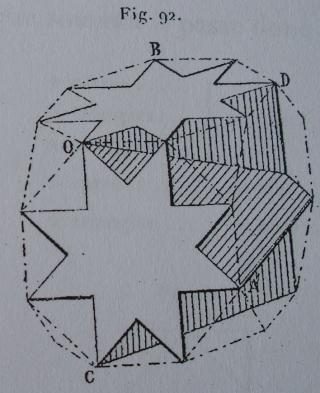
Ce polyèdre à été découvert par Miller, c'est le seul polyèdre uniforme que l'on ne peut pas construire par la méthode de Wythoff
Il a été publié la première fois en 1954 dans l'article Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450
Coxeter, H.S.M., Longuet-Higgins, M.S., Miller, J.C.P., Uniform Polyhedra. Phil. Trans. 1954, 246A, 401-450 fig 92
p.200-203 de Polyhedron Models
Fin provisoire de cet article
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 210 autres membres