Polyèdres (l'article)
Voici une nouvelle page sur les polyèdres
Cette page est réalisée par Jean-Jacques Dupas (toutes les photos de cette page, sauf celles qui proviennent d'autres sites, sont © Jean-Jacques Dupas, toute utilisation, même partielle, de matériel provenant de cette page, photos, textes... ne peut être utilisée sans l'accord écrit de Jean-Jacques Dupas )
En exclusivité pour les visiteurs du blog voici mes dernières réalisations, puisque je n'ai jamais exposé ces nouveaux modèles:
Un simple dodécaèdre régulier fini le 08 février 2015 mais à la manière de

Léonard de Vinci dans "de Divina Proportione" de

Luca Pacioli ( le personnage central, on remarque un petit rhombi cuboctaèdre de verre à moitié rempli d'eau en haut à gauche et un dodécaèdre en bas à droite)
après ces remarques mon modèle. Ce n'est pas très visible mais chaque arête possède une épaisseur
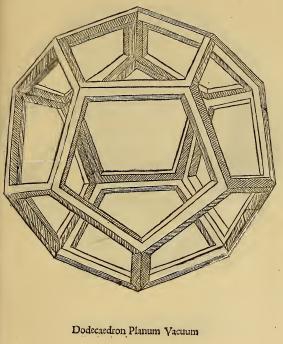
mon modèle Celui de Léonard le "Dodecacedron planus Vacuum"
Le 15 février 2015 j'ai construit un autre modèle en assemblant
30 arêtes, vue ici de l'intérieur avec
20 cornières matérialisant les sommets, les cornières sont glissées à l'intérieur des arêtes. Cela donne un
magnifique dodécaèdre d'arête 11 cm de longueur et de 14 mm d'épaisseur
Dans la foulée le 21 février 2015 et dans le même esprit j'ai construit un tétraèdre (Cf. si dessous) à côté le tetracedron planus vacuus de Léonard
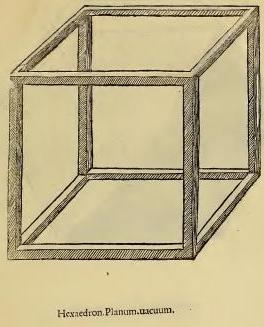
puis début avril 2015 un simple cube (je dis simple mais il ne faut pas sous-estimer le cube et le méconnaître car le cube possède un nombre incroyable de propriétés)
Je vais vous détailler la construction :
J'ai d'abord dessiné les arêtes
puis les cornières des sommets
Une fois collée voici la cornière de sommet
l'assemblage peut commencer, on introduit la cornière de sommet dans le barreau d'arête
remarquez les languettes des barreaux permettant de cacher les trous des cornières, ces languettes rendent la construction plus difficile, elles ne sont pas indispensables.
continuons le carré de base
à part, on prépare un barreau avec ses deux cornières

l'assemblage ne pose pas de problème
Quand on a le carré de base on ajoute un premier montant,
puis un second,
enfin le quatrième,
à part on construit un autre carré, identique à celui de tout à l'heure, j'ai changé de table d'assemblage.
Et voilà un magnifique cube à la manière de Léonard (son cubus planus vacuus)
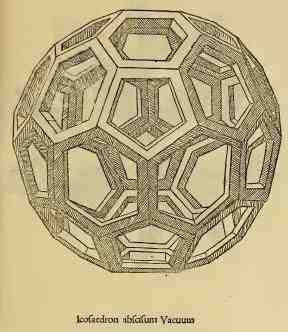
Le 11 et 12 avril 2015 suivant la même méthode, je me suis lancé dans un défi beaucoup plus impressionnant la construction d'un icosaèdre tronqué. Voici celui de Léonard son icosaedron Abscisus Vacuus.


Ce solide comporte 60 sommets, 90 arêtes (30 séparant 2 hexagones et 60 séparant un hexagone et un pentagone)
La conception bien que subtile m'a pris 2 h. La grosse difficulté est que les arêtes sont de deux types, celles partagées entre deux hexagones sont symétriques, alors que celles séparant un hexagone et un pentagone ne le sont pas. Enfin les cornières qui s'insèrent à chaque sommet ont toujours 2 branches sur pentagone et une branche sur hexagone. Le solide final fait 50 cm de diamètre, mais les arêtes sont trop fines il faut que je les fasse plus épaisses la prochaine fois afin d'avoir un solide moins fragile et plus proche de celui de Léonard de Vinci.
Aussitôt dit, aussitôt redémarré
Ci-dessus l'arête entre un pentagone et un hexagone. L'hexagone est en haut, remarquez les détrompeurs (les 2 encoches circulaires) signalent les côtés hexagonaux
Ci-dessus l'intérieur du sommet
Ci-dessus le sommet une fois assemblé
Ci dessus le même sommet retourné
Ci-dessus, sur l'intérieur du sommet on assemble l'extérieur, cela donne un sommet plus rigide et moins vide

l'assemblage peut commencer, on monte l'arête hexagone-hexagone, j'aurais dû y mettre des détrompeurs pour être homogène
puis les deux arêtes pentagone-hexagone, avec un vieux fond de colle je n'ai pas été très propre
Ce qui permet de construire le premier pentagone
Puis on avance
Et j'ai enfin fini le 07 mai 2015
Les proportions sont bien meilleures, le modèle est très rigide et beaucoup plus solide ! Le problème c'est que j'ai fait plusieurs erreurs au montage, la première c'est que j'ai tout collé au fur et à mesure, le modèle devient trop rigide donc difficile d'insérer les nouvelles pièces. En plus je me suis trompé sur un assemblage donc difficile à rattraper. Enfin j'aurais dû mettre des détrompeurs plus discrets (un petit trait de pli par exemple) et uniquement sur les branches de pentagone.
Polyèdres uniformes
Je voue une véritable passion aux polyèdres uniformes, j'ambitionne de tous les construire
Rappelons que les polyèdres uniformes sont des polyèdres composés de polygones réguliers au sens large (on admet les étoiles) dont les sommets sont transitifs (il existe un groupe de symétrie, qui transforme un sommet en tous les autres) cette famille nombreuse comprend:
- les solides de Platon W1 -> W5 (tous construits)
- les solides archimédiens W6 -> 18 (tous construits)
- les étoiles de Kepler-Poinsot W20, W21, W22, W41 (tous construits)
- les prismes réguliers, c'est une famille infinie
- les antiprismes réguliers c'est une famille infinie
- les antiprismes réguliers croisés c'est une famille infinie
- les autres non camus W67 -> W109 (tous construits sauf W88, W96, W98, W101, W105, W108, W109)
- les camus W110 -> W119
La numérotation Wx fait référence à la numérotation de mon ami Magnus Wenniger dans Polyhedron Models
Un W90 20 hexagones 12 décagones fini le 12 novembre 2014, 380 pièces! Le diagramme décrivant les intersections dans le décagone est dans Polyhedron Models de mon ami Magnus Wenniger, mais il est partiellement faux!
Bien que l'ayant construit assez gros, ce n'était pas encore assez car les pentagrammes sont tous petits
Le W95 un grand icosaèdre tronqué 20 {6} et 12 {5/2} soit 20 hexagones et 12 pentagrammes que j'ai fini le 1 novembre 2014, 192 pièces seulement
J'avoue que je l'ai construit un peu petit donc j'ai eu beaucoup de mal pour le finir proprement car les pièces sont très petites
Le W87 20 triangles et 12 pentagones fini le 28 octobre 2014, 294 pièces!
Un modèle très difficile à réaliser, car il faut aligner tous les triangles!
Un W106 fini le 22 octobre 2014
20 triangles et 12 étoiles à 10 branches, 180 pièces seulement!
Un W102 12 pentagones 10 hexagones fini le 29 août 2014, 312 pièces
Les creux sont très profonds ce qui rend ce modèle très difficile à réaliser
un W100 12 pentagones et 10 hexagones
Je l'ai construit beaucoup trop petit 15cm de diamètre en 11 couleurs
modèle très difficile à réaliser car les 10 hexagones, une couleur pour chaque, sont équatoriaux, le centre du polyèdre est très encombré, de plus les coupes hexagonales sont reliées entre elles par une arête.
Quelques constructions pour noël exécutés le 14 novembre 2015
Un W73 de noël
une étape de la construction
sur le même principe un W70 de noël

Un triacontaèdre rhombique, le dual du W73, fini début juillet 2019. C'est un triacontaèdre rhombique puisque constitué de 30 losanges entre-croisés des sommets sont à l'intérieur du polyèdre.
J'ai commencé avec 5 vrais losanges entiers puis avec des morceaux.
C'est aussi une étoile du triacontaèdre rhombique, le polyèdre de Catalan
justement à propos de ce polyèdre j'ai contruit l'étoile finale, je l'ai fini le 12 juillet 2019
Le polyèdre est constitué de barreaux à section carrée qui s'appuient sur les 5 cubes du dodécaèdre!

vue suivant les axes d'ordre 3

Vue suivant les axes d'ordre 5
Voici 3 vues, à cause de la chaleur du début du mois j'ai eu des problèmes avec la colle et j'en ai mis partout! Bon mais c'est une maquette d'un modèle impressionant avec ses 120 pointes.
Début septembre 2019 j'ai fait un modèle tressé du triacontaèdre rhombique.
Je commence par 5 barreaux
Puis j'ajoute les 5 barreaux suivants
Je continue avec les 5 suivants
Puis les 5 barreaux orange
Enfin les 10 barreaux manquants
Les disques rouges servent à maintenir les barreaux en place, il faut que je colle l'intérieur et que j'enlève ces disques, c'est un super modèle très spectaculaire avec ses 30 barreaux de 6 couleurs les couleurs sont par directions les 6 diagonales de l'icosaèdre
Toujours en septembre 2019 je suis revenu sur le dodécaèdre rhombique et son étoile à l'infini
Une vue suivant les hexagrammes
Puis une vue suivant les carrés
Pour le fun je n'ai gardé que les prismes en hexagrammes, je dis pour le fun car c'est une croix avec des étoiles de David
Une autre vue:
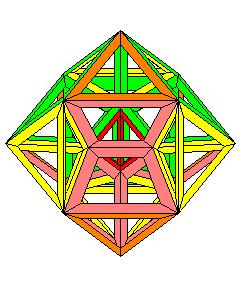
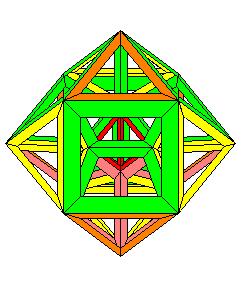
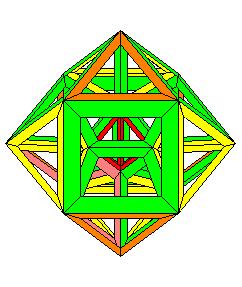
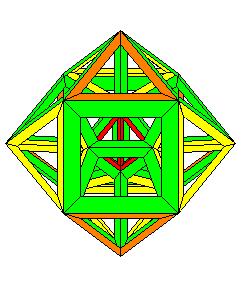
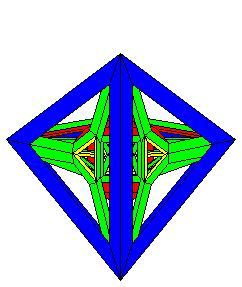
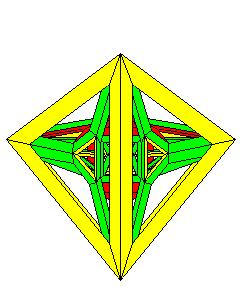
Pendant que j'y étais j'ai fait l'étoile à l'infini du dodécaèdre régulier. Cette étoile est composée de 30 barreaux à section rhombique :
c'est une vue suivant l'axe d'ordre 5

Une autre vue suivant un axe d'ordre 3, et oui le noyau convexe de cette étoile est un triacontaèdre rhombique !
Décembre 2019 construction du W119
Un petit tour dans la quatrième dimension
En dimension 4 il y a 6 polytopes réguliers
- Le simplexe 4 ou hyper tétraèdre
- le 16 cellules ou hyper-octaèdre (le cube est l'une des projections orthogonales de l'hyper-octaèdre)
- le 8-cellules ou hyper-cube (le cube, le dodécaèdre rhombique, le prisme à base hexagonales sont des projections orthogonales de l'hyper-cube)
- le 24 cellules
- le 120 cellules
- le 600 cellules
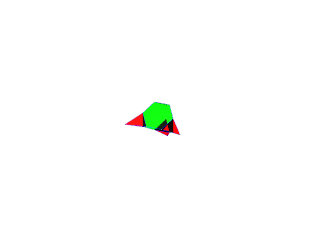
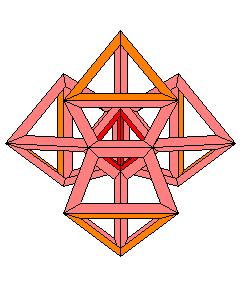
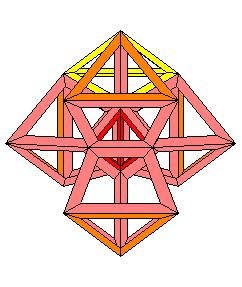
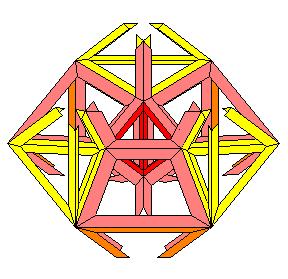
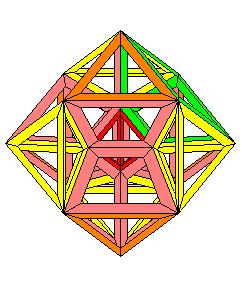
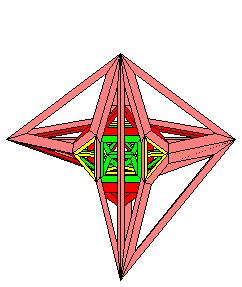
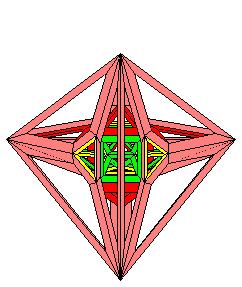
Un hyper-octaèdre ou 16-cellules ou β4 suivant H.S.M. Coxeter
Projection stéréographique de pôle situé au dessus d'une cellule tétraédrique
1 tétraèdre central bleu
4 tétraèdres oranges s'appuyant sur le tétraèdre central
6 tétraèdres jaunes entre les tétraèdres oranges
4 tétraèdres jaunes s'appuyant sur le tétraèdre externe mais vers l'intérieur
1 tétraèdre bleu externe
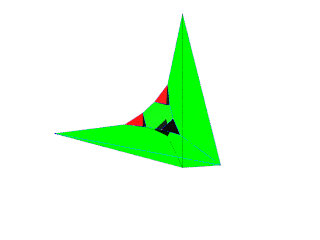
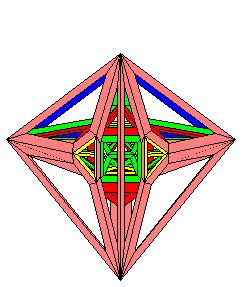
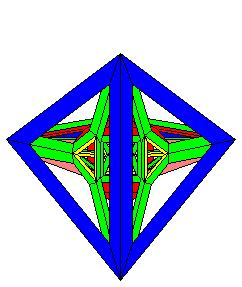
Le tétraèdre central bleu vu en vraie grandeur

un premier tétraèdre orange, lui est déformé

On referme par le tétraèdre bleu, vu en vraie grandeur sous le pôle de projection
En dimension 4 il existe plus de 40 polytopes archimédiens c'est-à-dire composés de polyèdres réguliers ou semi réguliers
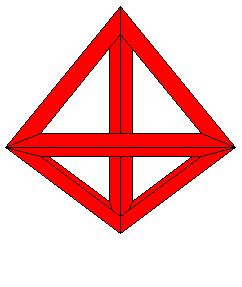
Mon premier polytope archimédien de la 4ème dimension un t1alpha4 (suivant la nomenclature de H.S.M. Coxeter) découvert en 1900 par Thorold Gosset
Ce polytope semi-régulier est composé uniquement de polyèdres réguliers octaèdres et tétraèdres:
Un polyèdre du groupe de l'hyper-tétraèdre composé de:
- 5 cellules tétraédriques
- 5 cellules octaédriques
- 10 faces triangulaires partagées chacunes par un tétraèdres et un octaèdre
- 20 faces triangulaires partagées chacunes par deux octaèdres
- 30 arètes
- 10 sommets
Une première projection stéréographique au dessus d'une cellule tétraédrique
Tétraèdres jaunes et octaèdres rouges
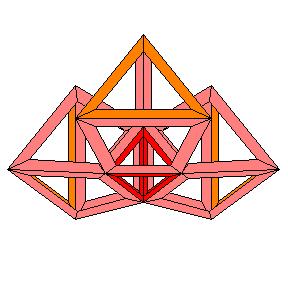
1 octaèdre rouge central
4 tétraèdres jaunes s'appuyant sur l'octaèdre central (une face sur deux)
4 octaèdres rouges s'appuyant sur l'octaèdre central (une face sur deux)
1 tétraèdre jaune externe
Une deuxième projection stéréographique au dessus d'une cellule octaédrique
1 tétraèdre jaune central
4 octaèdres rouges s'appuyant sur le tétraèdre central
4 tétraèdres jaunes entre les 4 octaèdres
1 octaèdre rouge externe
Mon deuxième polytope archimédien de la 4ème dimension un t01alpha4 suivant la nomenclature de H.S.M. Coxeter
Constitué de :
- 5 tétraèdres tronqués
- 5 tétraèdres réguliers
- 10 hexagones réguliers partagés par deux tétraèdres tronqués
- 20 faces triangulaires partagées chacunes par deux tétraèdres
- 40 arêtes
- 20 sommets
J'ai construit le 27 février 2016 une projection stéréographique dont le pôle est au dessus d'un tétraèdre
On commence par un tétraèdre tronqué rouge celui qui est le plus éloigné du pôle, il est vu en vraie grandeur. Ce tétraèdre tronqué est tout petit
Une autre vue de ce tétraèdre tronqué
La construction de 4 tétraèdres jaaunes déformés par la projection
Les 4 tétraèdres jaunes sont assemblés
On construit un grand tétraèdre tronqué rouge déformé par la projection

Les 4 assemblés
On referme par le tétraèdre régulier jaune, vu en vrai grandeur, juste en dessous du pôle
Le tétraèdre tronqué du centre
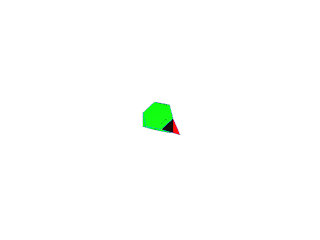
Puis 2 tétraèdres tronqués verts
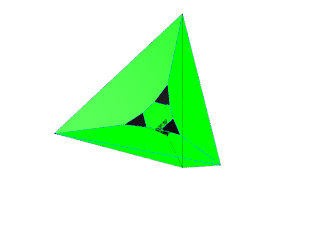
Enfin on referme avec le dernier tétraèdre rouge qui semble enfermer les autres polyèdres de l'assemblage
Mais le pôle aurait pu se situer juste au dessus d'une face en forme de tétraèdre tronqué
ce que j'ai fini le 29 février 2016
On commence par le tétraèdre central jaune qui est régulier et tout petit

Puis un tétraèdre tronqué rouge déformé par la projection, il est beaucoup plus gros

puis les tétraèdres jaunes qui sont aussi déformés

un deuxième tétraèdre tronqué rouge

le dernier tétraèdre jaune ils sont bien 5, un au centre et quatre autres

les tétraèdres tronqués rouges, ils sont 4 pour l'instant

et enfin le cinquième tétraèdre tronqué rouge dans lequel les autres polyèdres semblent enfermés
La semaine prochaine nous construirons un autre polytope archimédien uniquement composé de tétraèdres tronqués
Comme promis la semaine dernière, nous sommes le 5 mars 2016, voici le t12alpha4 suivant la nomenclature de H.S.M. Coxeter
Un polytope semi-régulier uniquement composé d'un seul type de polyèdres semi-réguliers des tétraèdres tronqués
Constitué de :
- 10 tétraèdres tronqués
- 20 hexagones réguliers
- 20 triangles
- 60 arêtes
- 30 sommets
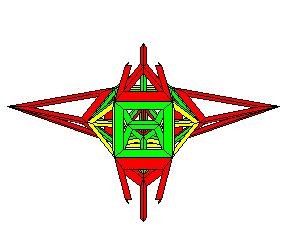
Voici une projection stéréographique, le pôle se situe au dessus du centre d'une cellule en forme de tétraèdre tronqué
En projection stéréographique les 10 tétraèdres tronqués se répartissent en une couche centrale constitué d'un tétraèdre tronqué, une couche de 8 tétraèdres tronqués, projetés en deux types, enfin une couche externe d'un tétraèdre tronqué refermant l'hypersolide.
La première couche est constituée d'un tétraèdre tronqué rouge, vu en vraie grandeur, car dans l'axe de la projection à l'opposé du tétraèdre tronqué sous le pôle de projection.
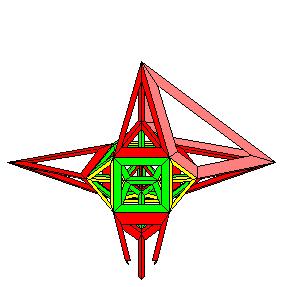
La deuxième couche est constituée de deux types de tétraèdres tronqués, 4 oranges et 4 jaunes. Les jaunes s'appuient sur les triangles du tétraèdre tronqué central alors que les oranges s 'appuient sur les hexagones du tétraèdre tronqué central.
Ces tétraèdres tronqués sont déformés par la projection stéréographique.
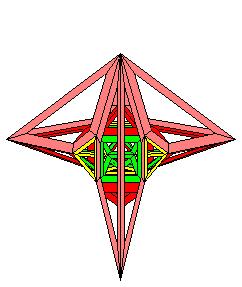
On contine, avec un tétraèdre tronqué jaune

Nous avons la forme du tétraèdre tronqué externe qui referme l'hyper-solide

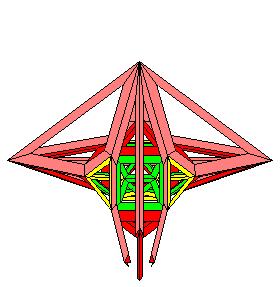
Vu de dessus dans l'axe des faces nous avons une succession de triangles et d'hexagones, cette succession existe aussi dans la 4ème dimension où toutes les cellules ont la même taille, c'est une fibration
le 6 mars 2016. J'ai commencé à étudier un autre polytope archimédien le t03alpha4 suvant la nomenclature de Coxeter
Il est constitué de 10 tétraèdres et 20 prismes à base triangulaire
voici sa projection stérégraphique avec un pôle au dessus du milieu d'un tétraèdre
On démarre par un tétraèdre rouge, le tétraèdre opposé au tétraèdre sous le pôle de projection
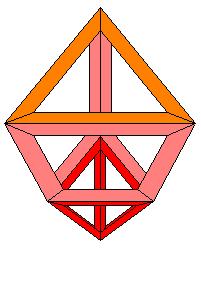
Sur ce tétraèdre on monte un prisme à base triangulaire les carrés sont roses, le triangle orange est aussi équilatéral
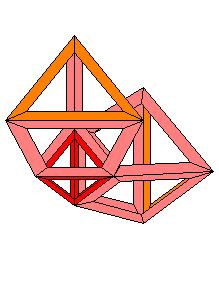
entre les prismes on monte un tétraèdre jaune
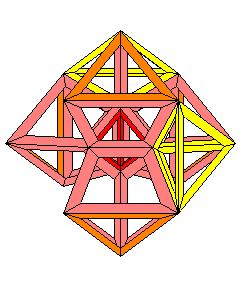
puis un trosième, attention la figure est un peu coupée
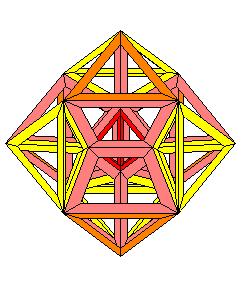
puis un quatrième, nous avons 6 creux
on peut y loger un prisme, le carré extérieur est un carré en projection
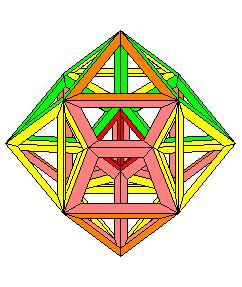
enfin un 6ème, remarquez que nous avons un magnifique cuboctaèdre

sur certaines faces triangulaires, 4 permi les 8, celles qui proviennent des prismes, car les triangles sont toujours partagés par un tétraèdre et un prisme, nous montons un tétraèdre très déformé par la projection
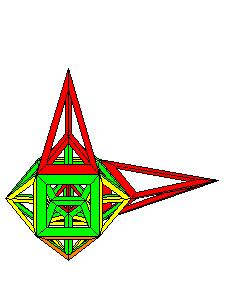
Maintenant au tour d'un prisme sur les carrés restants
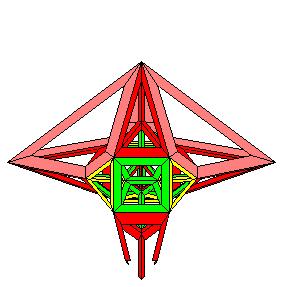
un cinquième
Il reste des triangles de libres sur lesquels on monte d'autres prismes, les grans triangles bleus sont équilatéraux
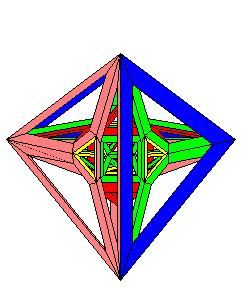
Enfin le dernier tétraèdre jaune
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 202 autres membres