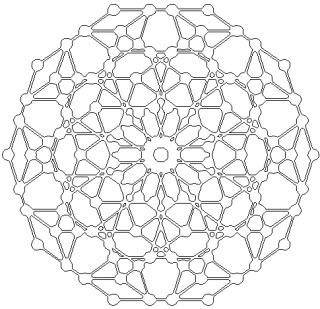
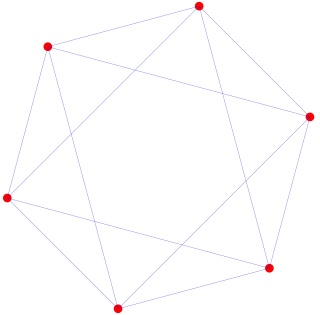
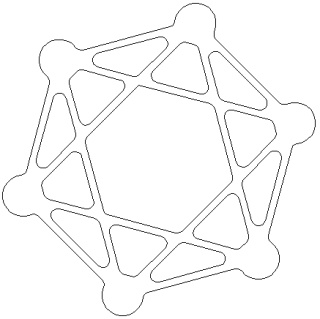
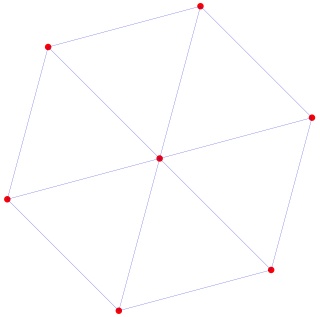
Mandalas polytopiques
Un article très visuel de Jean-Jacques Dupas qui peut se deguster sans aucune connaissance mathématique.
Étymologiquement le terme mandala provient du sanskrit « cercle », ils sont utilisés pour la méditation. Quoi de plus sympa que de méditer sur les projections des polytopes. Évidement nous pouvons construire des mandalas grâce aux polyèdres ou à leurs homologues des dimensions supérieures les polytopes. Comme cela vous méditerez sur des objets venus de dimensions supérieures. Cool non !
En Dimension 0 il y a le point.
En Dimension 1, il y a le segment de droite
En Dimension 2, il y a le polygone composé de segments de droite, chaque sommet est partagé par 2 segments
En dimension 3, il y a le polyèdre composé de polygones, chaque arête est partagée par 2 polygones
En dimension 4, il y a le polytope (mot forgé par Alicia Boole-Stott) composé de polyèdre, chaque face est partagée par 2 polyèdres.
……………………….
En dimension n, il y a le polytope de dimension n composé de polytopes de dimension n-1, chaque sous-polytope de degré n-2 est partagé par 2 polytopes de degré n-1
Quand on projette un polytope de dimension n sur un plan la figure n'est pas toujours très « régulière ».
Il y a des opérations de l'espace qui laissent invariant un polytope. Par exemple une rotation de 120° autour d'un axe passant par deux sommets opposés d'un cube. Par exemple une rotation de 90° autour d'un axe passant par le centre de deux faces opposées du cube. En fait pour le cube il existe 48 transformations (dont l'identité) qui le laisse invariant on parle de groupe de symétrie. Les plus élémentaires de ces opérations sont l'identité, des symétries dans un plan (9 dans le cas du cube), des rotations( rotation de 180°, 120°,90° dans le cas du cube), mais aussi des compositions de rotations…
Quand un polytope possède un groupe de symétrie, ce qui est le cas des polyèdres réguliers et semi-réguliers, il existe une projection orthogonale « particulièrement symétrique », la surprise c'est que l'ordre (Un carré possède une symétrie d'ordre 4 car le carré est invariant par une rotation de 360°/4) de sa symétrie prend une valeur particulière qui ne se devine pas comme cela !
Par exemple pour le cube notre projection possède une symétrie d'ordre 6.
Dans la table suivante nous avons la correspondance entre les groupes de symétries et l'ordre h de la projection la plus symétrique.
|
Groupe de symétrie |
h |
dimension |
|
|
An |
n+1 |
n>1 |
Groupe du tétraèdre(n=3), |
|
Bn |
2n |
n>2 |
Groupe du cube, octaèdre (n=3), hyper cube(n=4)... |
|
Dn |
2(n-1) |
n>3 |
|
|
E6 |
12 |
6 |
|
|
E7 |
18 |
7 |
|
|
E8 |
30 |
8 |
|
|
F4 |
12 |
4 |
Groupe du 24-cellules |
|
H3 |
10 |
3 |
Groupe Icosaédrique (du dodécaèdre, icosaèdre) en dimension 3 |
|
H4 |
30 |
4 |
Groupe de l'hyper-icosaèdre, hyper-dodécaèdre de la dimension 4 |
|
I2(h) |
h |
2 |
Groupe dièdre d'ordre h dans le plan |
Il n'y à plus qu'a regarder ce que vont nous donner nos chers polytopes réguliers et semi-réguliers pour faire des
mandalas (toutes les images sont copywright Jean-Jacques Dupas 2017)
Les premiers mandalas ne seront pas très spectaculaires, mais patience!
Groupe du tétraèdre A3 : les projections les plus symétriques possèdent une symétrie d'ordre 4
Le tétraèdre à gauche et sa version mandala à droite :
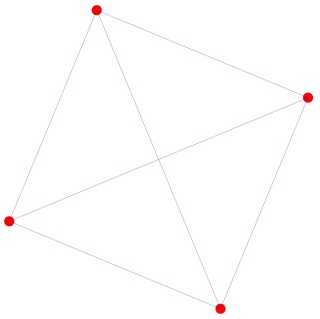
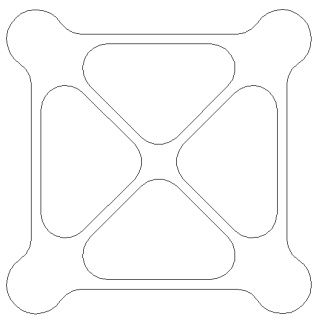
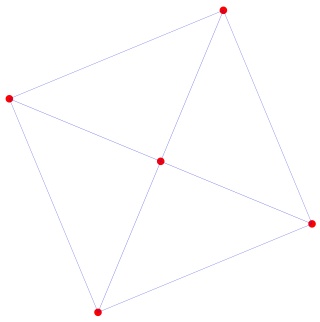
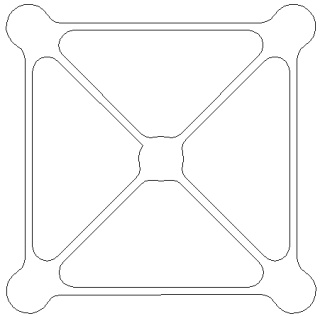
L'octaèdre (du groupe tétraédrique) à gauche et sa version mandala à droite (la différence c'est le point du milieu):
Le tétraèdre tronqué à gauche et sa version mandala à droite :
Le cuboctaèdes (du système tétraédrique) à gauche et sa version mandala à droite :
L'octaèdre tronqué (dans sa version tétraédrique) à gauche et sa version mandala à droite :
Comme promis passons à la symétrie d'ordre 5 pour cela étudions dans la dimension 4 le groupe de
l'hyper-tétraèdre A4 : les projections les plus symétriques possèdent une symétrie d'ordre 5
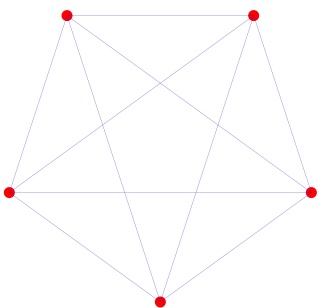
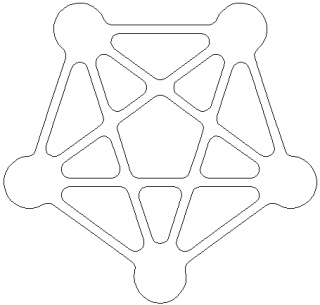
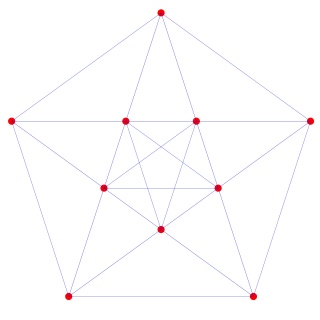
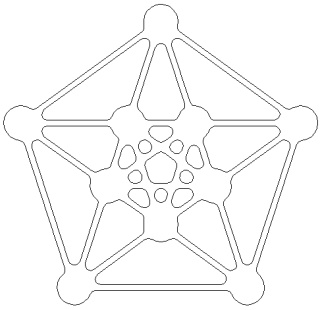
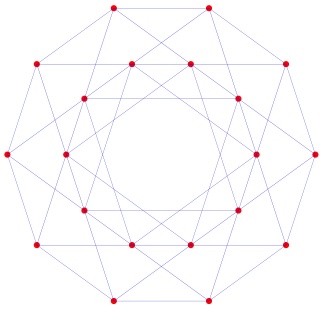
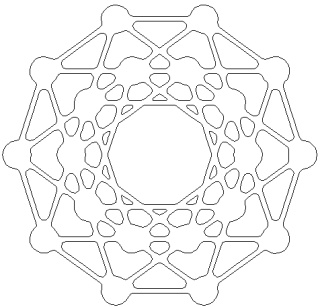
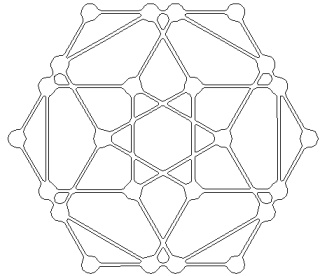
L'hyper-tétraèdre t0alpha4 ou t3alpha4 à gauche et sa version mandala à droite :
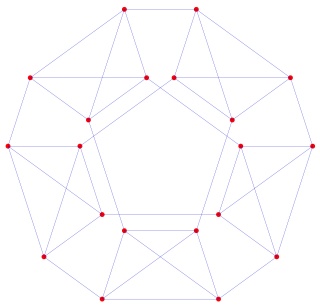
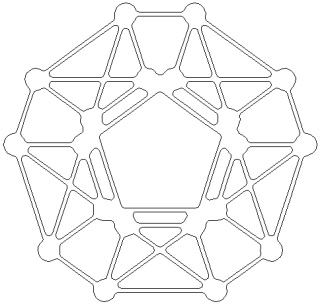
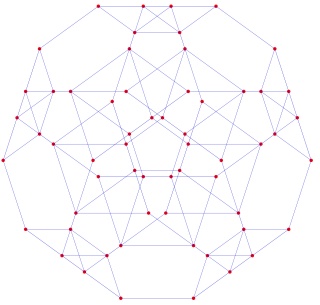
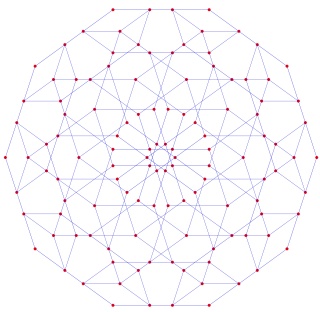
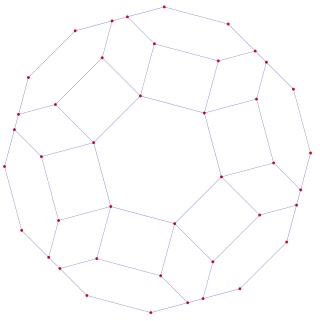
Le polytope t1alpha4 ou t2alpha4 à gauche et sa version mandala à droite :
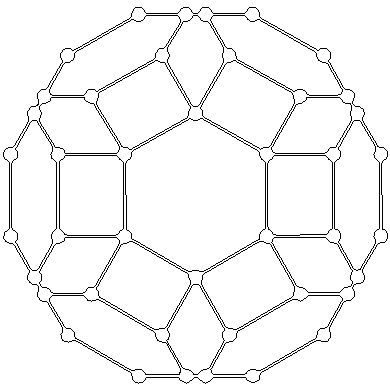
Le polytope t01alpha4 ou t23alpha4 à gauche et sa version mandala à droite :
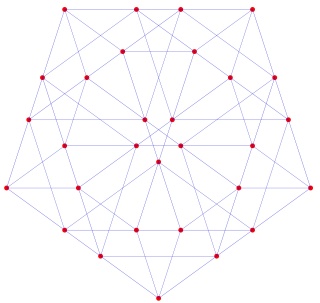
Le polytope t02alpha4 ou t13alpha4 à gauche et sa version mandala à droite :
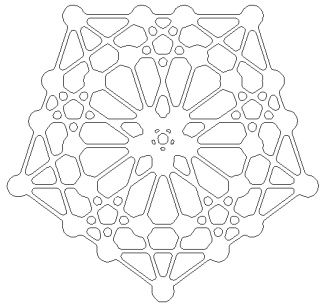
Le polytope t03alpha4 à gauche et sa version mandala à droite :
Le polytope t2alpha4 à gauche et sa version mandala à droite :
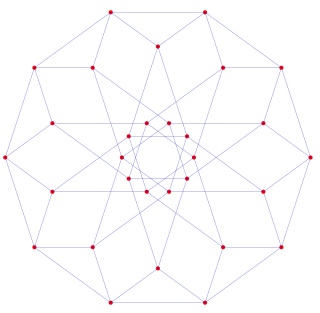
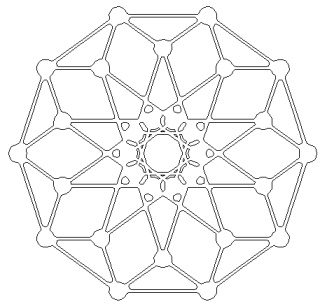
Le polytope t012alpha4 ou t123alpha4 à gauche et sa version mandala à droite à venir:
Le polytope t013alpha4 ou t023alpha4 à gauche et sa version mandala à droite :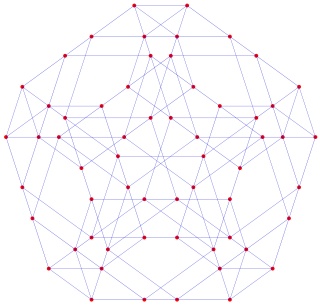
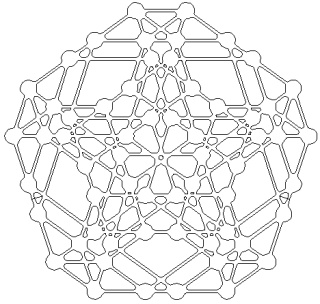
Le polytope t0123alpha4 ou polytope d'Hinton à gauche et sa version mandala à droite :
Passons à la symétrie d'ordre 6 pour cela on pourrait étudié dans la dimension 5 le groupe de l'hyper-tétraèdre A6 : mais plus facile étudions dans la dimension 3 le groupe de l'octaèdre B3
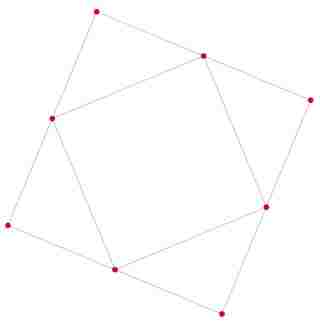
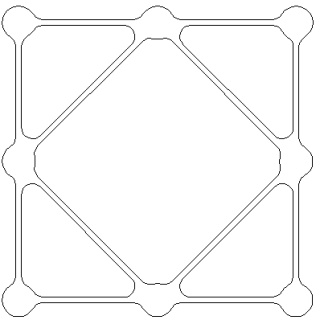
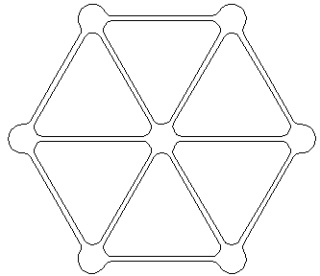
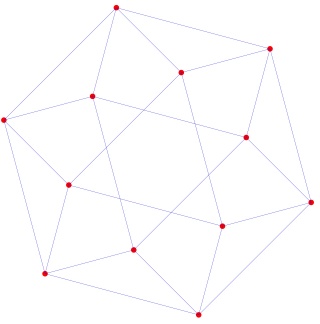
Justement l'octaèdre à gauche et sa version mandala à droite :
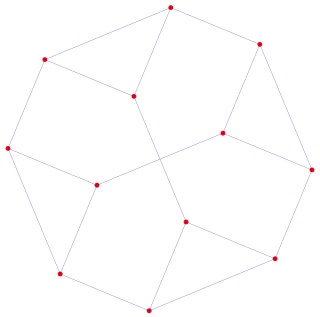
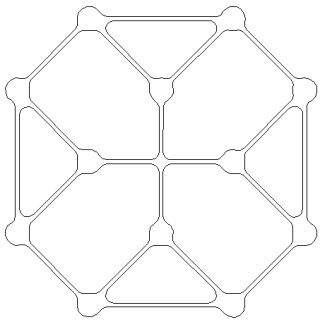
le cube à gauche et sa version mandala à droite :
le cuboctaèdre à gauche et sa version mandala à droite :
L'octaèdre tronqué à gauche et sa version mandala à droite :
Le cube tronqué à gauche et sa version mandala à droite :
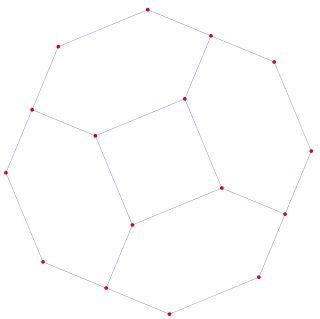
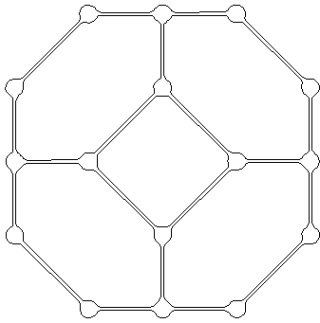
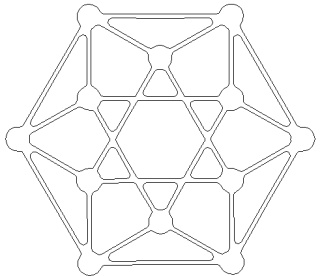
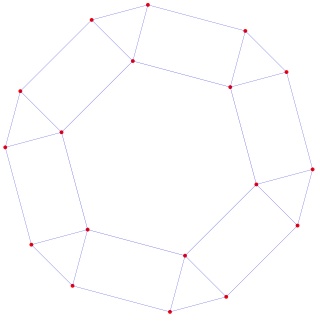
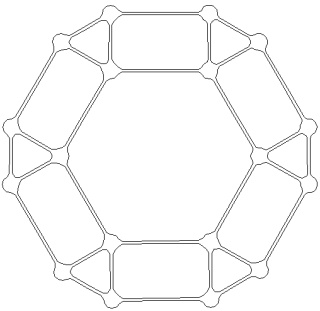
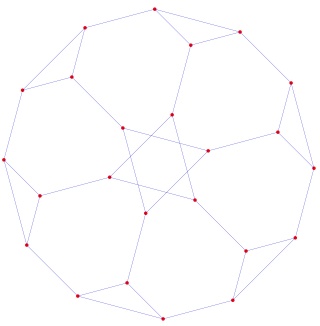
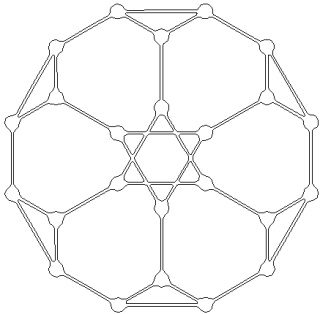
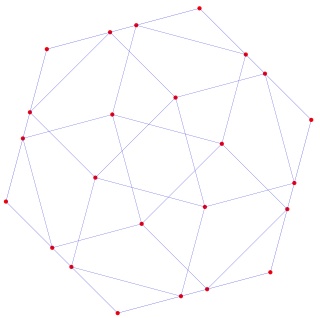
Le petit rhombicuboctaèdre à gauche et sa version mandala à droite :
Le grand rhombicuboctaèdre à gauche et sa version mandala à droite :
La suite dans l'article suivant Mandalas Poytopiques II (Mandalas Géométriques, Mandalas Mathématiques)
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 200 autres membres