Mandalas des Simplexes
Sous ce titre énigmatique Jean-Jacques Dupas vous fait découvrire des jolis "naperons" qui sont des projections des simplexes, la généralisation du triangle, tétraèdre....
Mais trève de blabla passons aux images
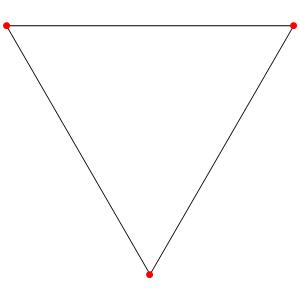
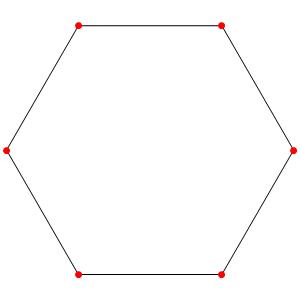
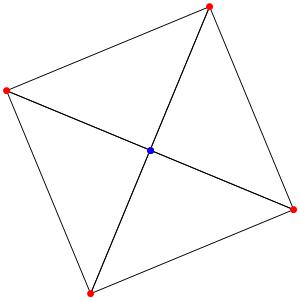
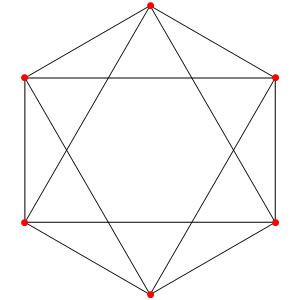
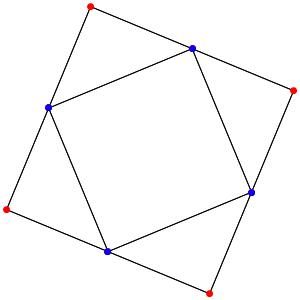
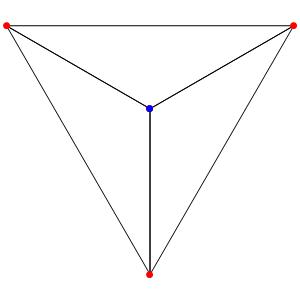
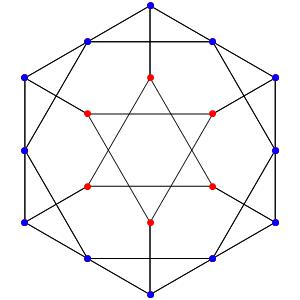
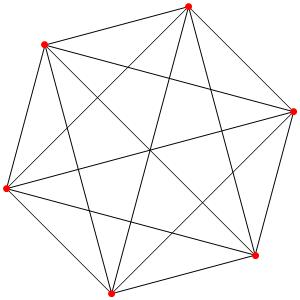
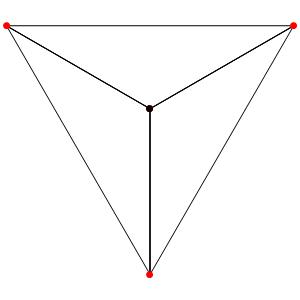
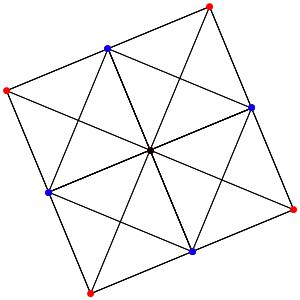
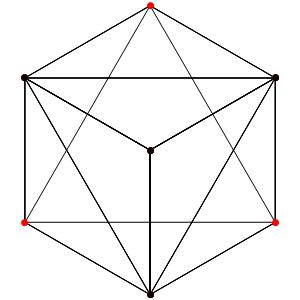
Commençons simplement avec les deux polygones réguliers du groupe A2: le triangle et l'hexagone, dans une symétrie d'ordre 3:
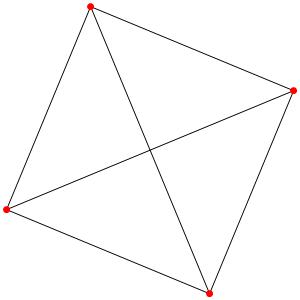
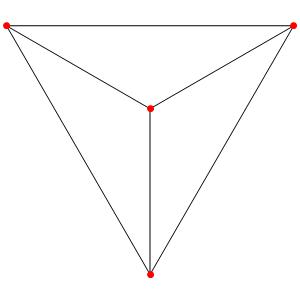
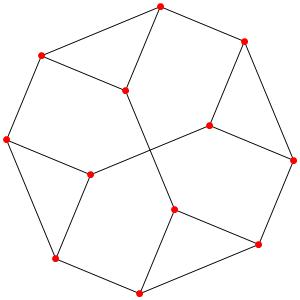
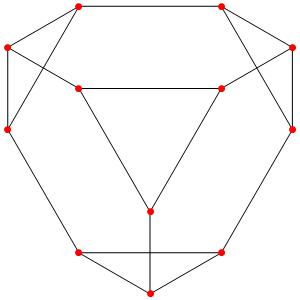
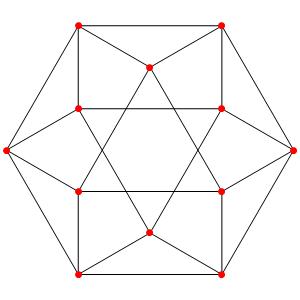
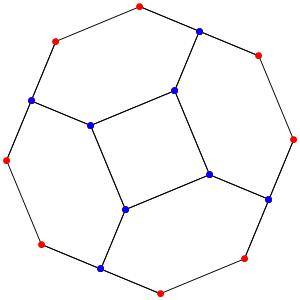
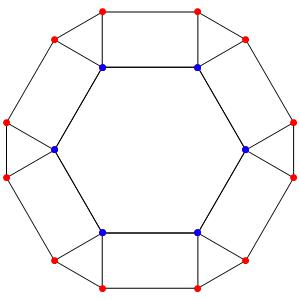
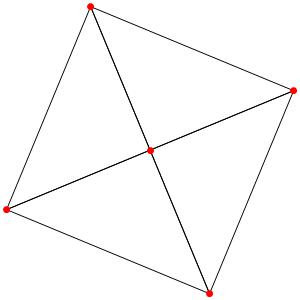
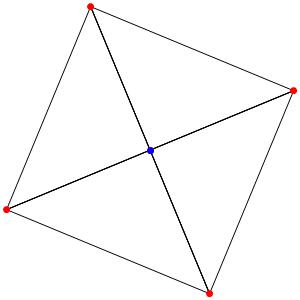
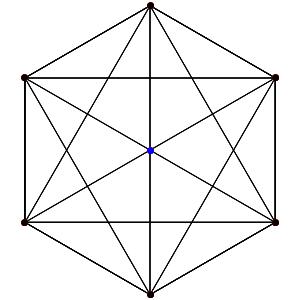
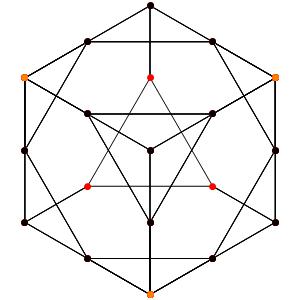
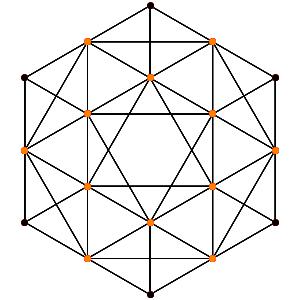
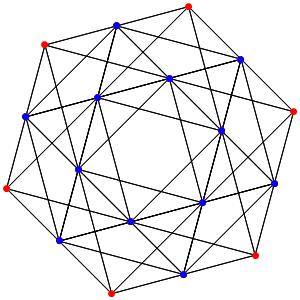
Passons à la dimension 3, les polyèdres réguliers et semi-réguliers du groupe A3 (Groupe tétraédrique). A gauche la symétrie d'ordre 4, à droite la symétrie d'ordre 3
Les points bleus sont des points doubles.
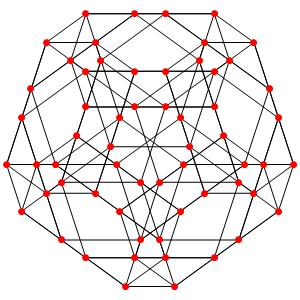
Octaèdre tronqué
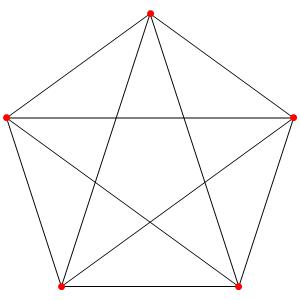
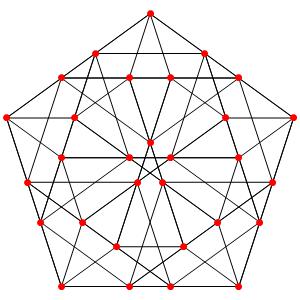
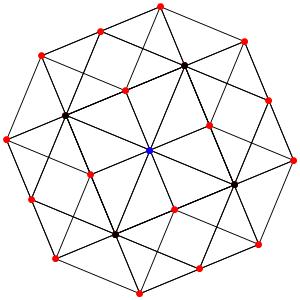
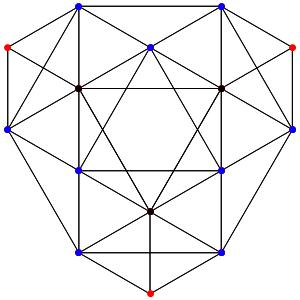
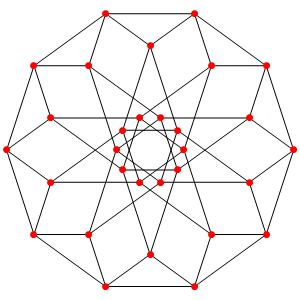
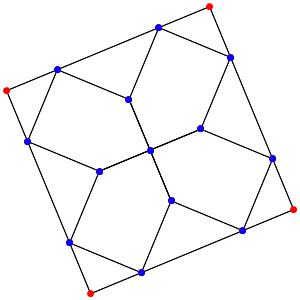
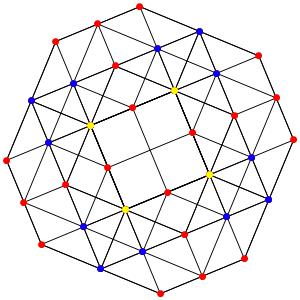
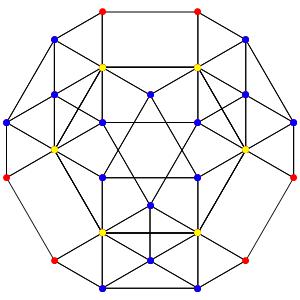
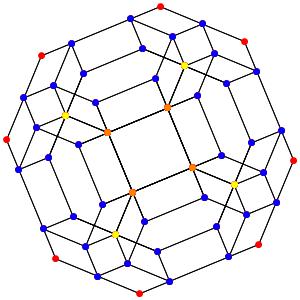
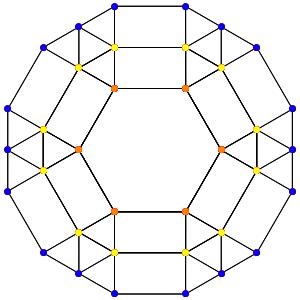
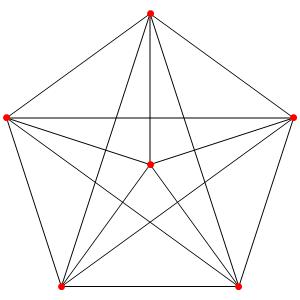
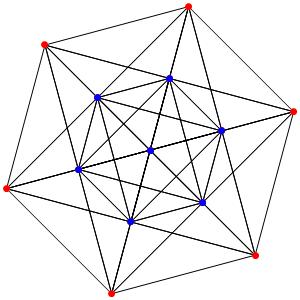
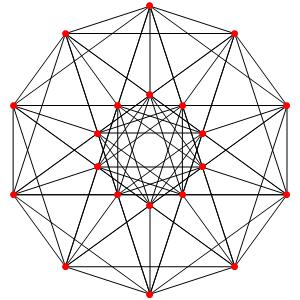
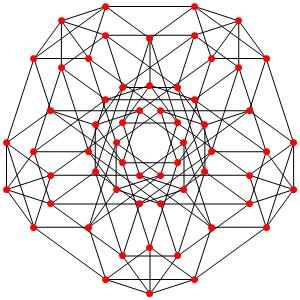
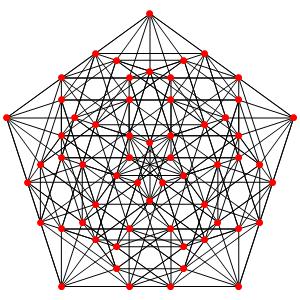
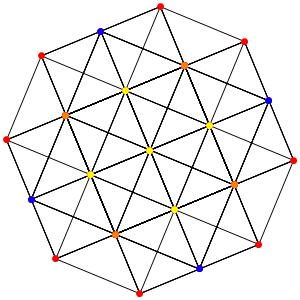
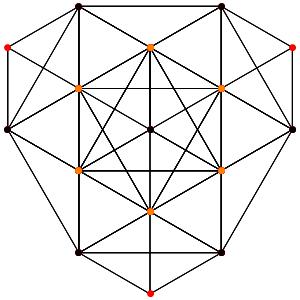
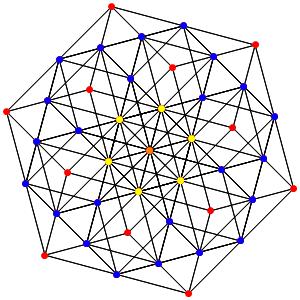
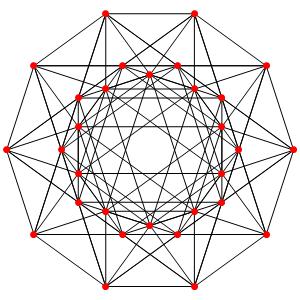
Super! La dimension 4, les polytopes réguliers et semi-réguliers du groupe A4. A gauche la symétrie d'ordre 5, puis au milieu la symétrie d'ordre 4, enfin à droite la symétrie d'ordre 3
Le t0α4
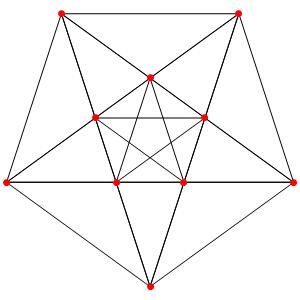
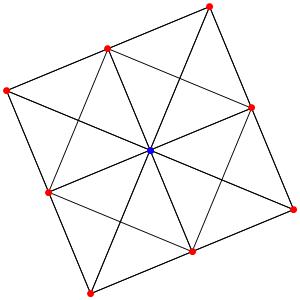
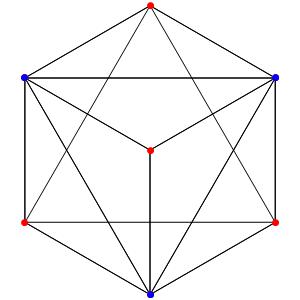
le t1α4
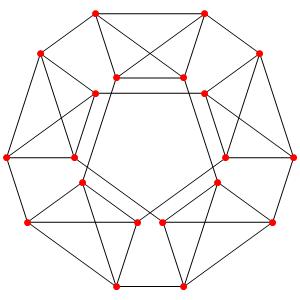
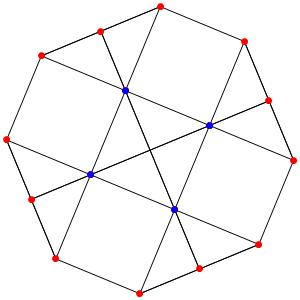
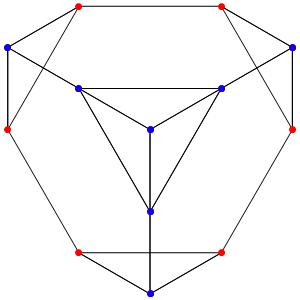
le t01α4
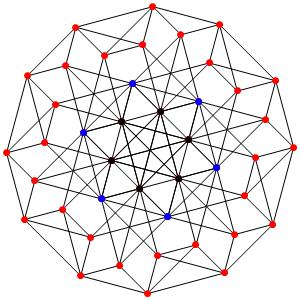
le t02α4 (points noirs = points triples)
le t12α4
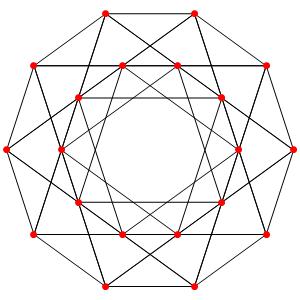
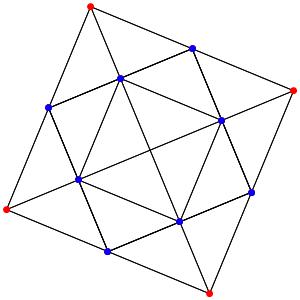
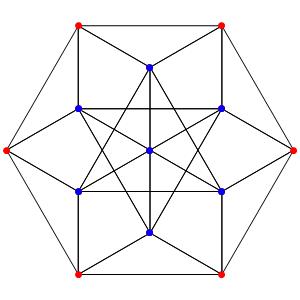
le t03α4
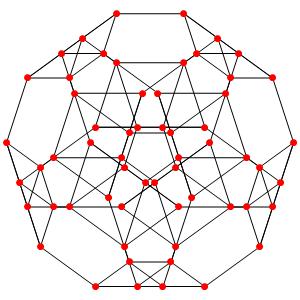
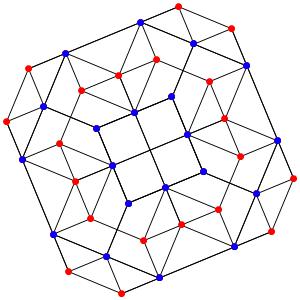
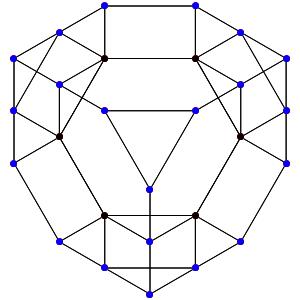
le tO12α4
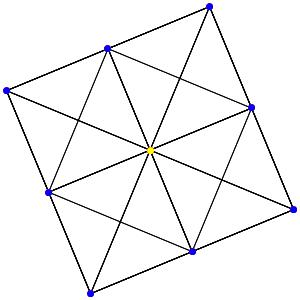
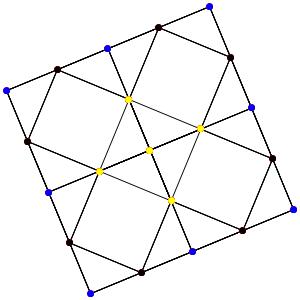
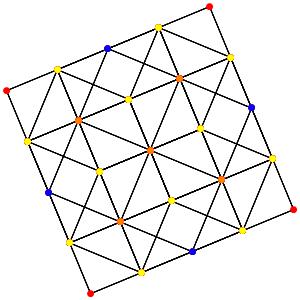
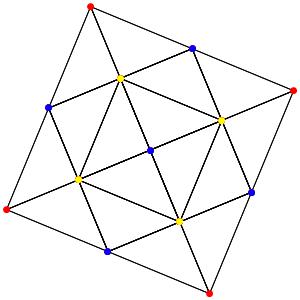
le t013α4 (points jaunes = points quadruples)
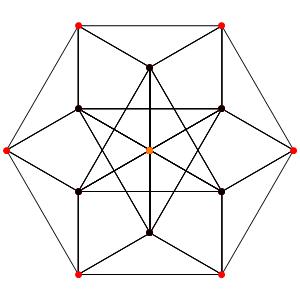
le t0123α4 ou polytope de Hinton ou permutoèdre (points oranges = points sixtuples)
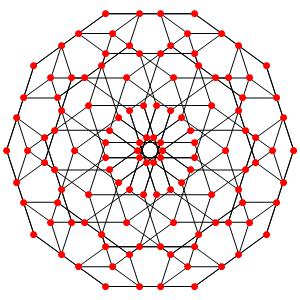
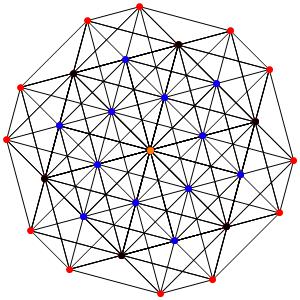
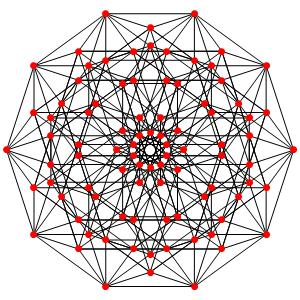
De mieux en mieux! La dimension 5, les polytopes réguliers et semi-réguliers du groupe A5. A gauche la symétrie d'ordre 6, puis la symétrie d'ordre 5, en suivant la symétrie d'ordre 4, enfin d'ordre 3
le t0α5
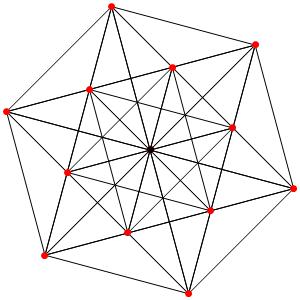
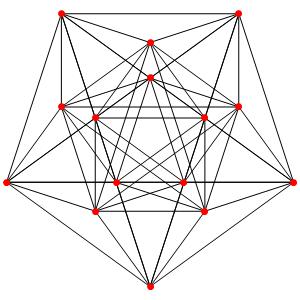
le t1α5
le t2α5
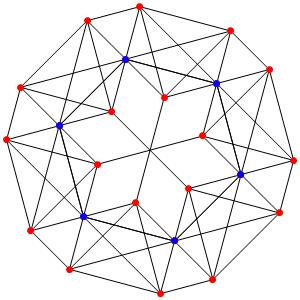
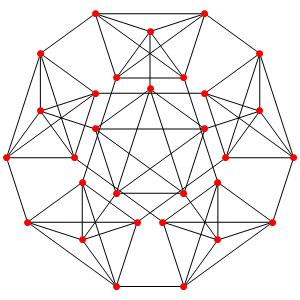
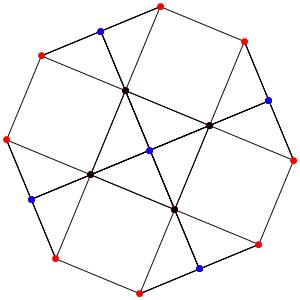
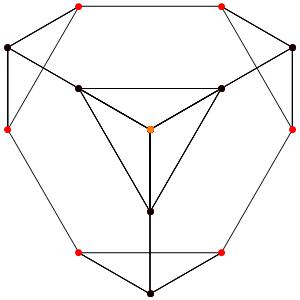
le t01α5
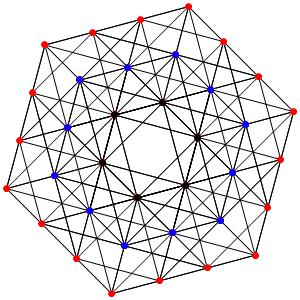
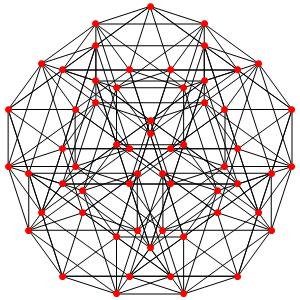
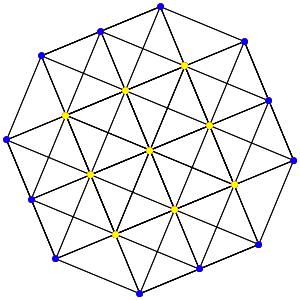
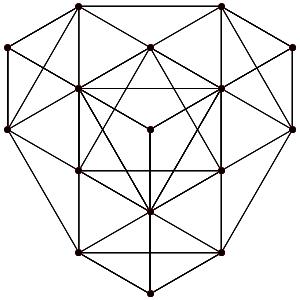
le t02α5
le t12α5
le t13α5
le t04α5
le t14α5
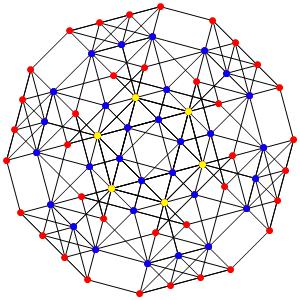
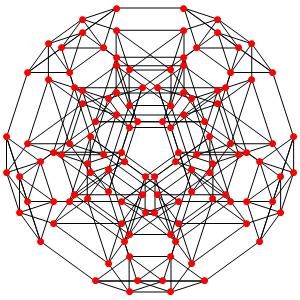
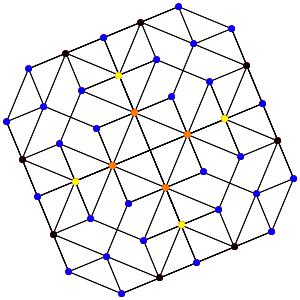
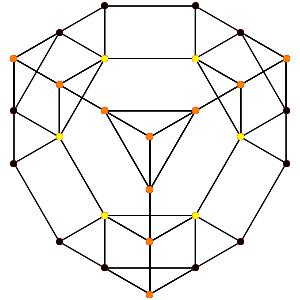
le t05α5
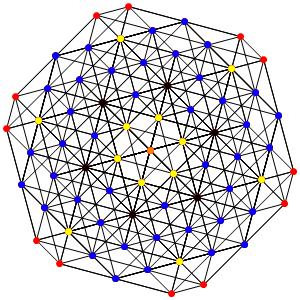
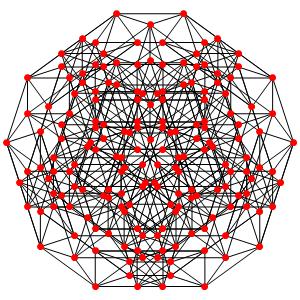
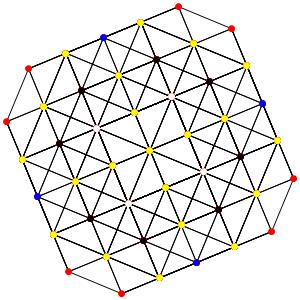
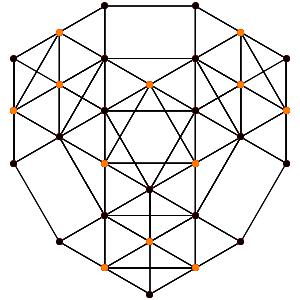
le t012α5 Ici les points noirs sont pentuples
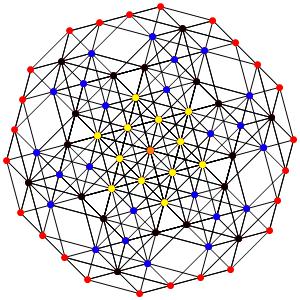
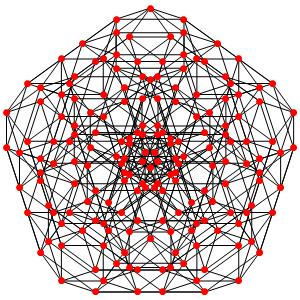
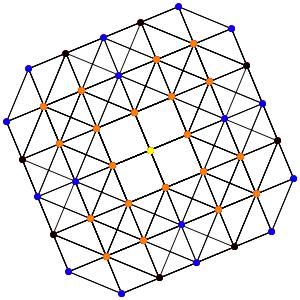
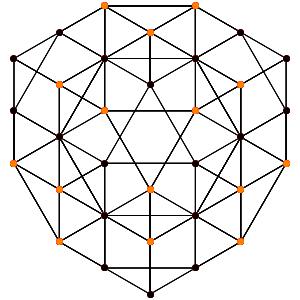
le t013α5, on revient à des points noirs triples
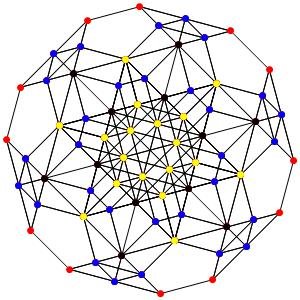
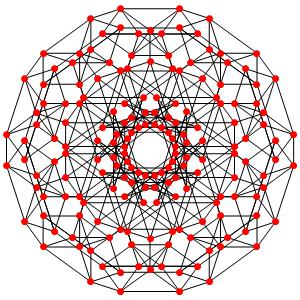
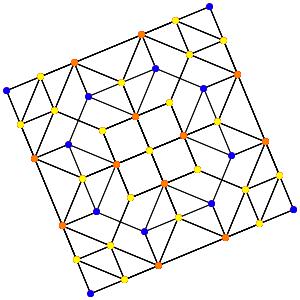
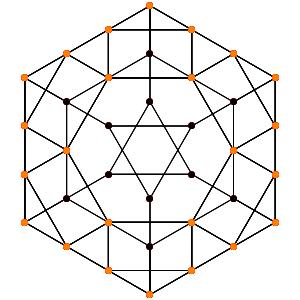
le t023α5
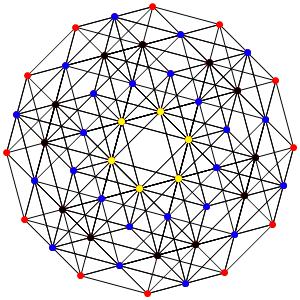
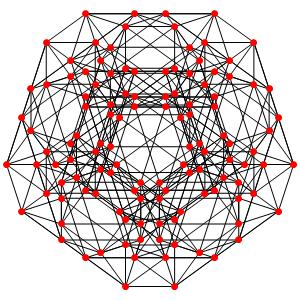
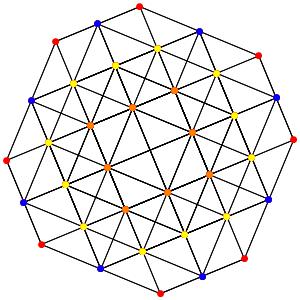
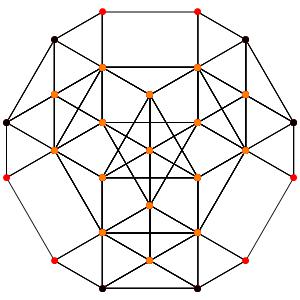
le t123α5
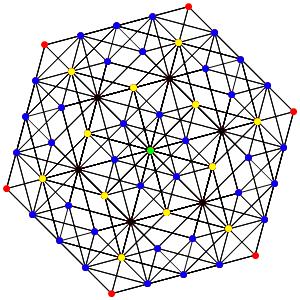
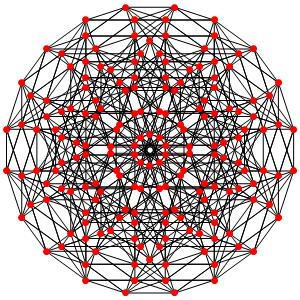
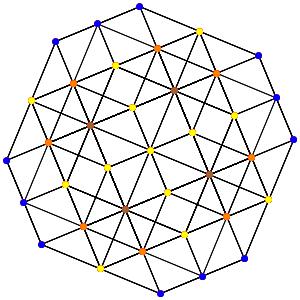
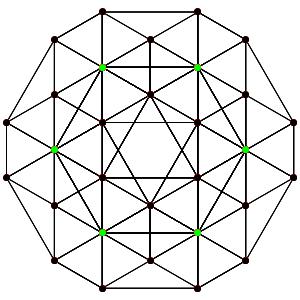
le t024α5 Le point vert est 12-uple les points noirs 7-uples
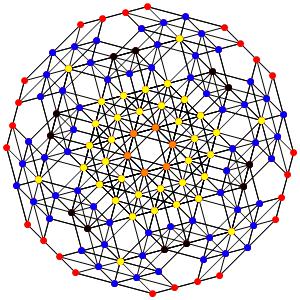
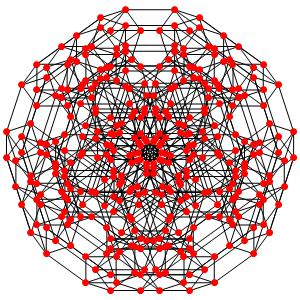
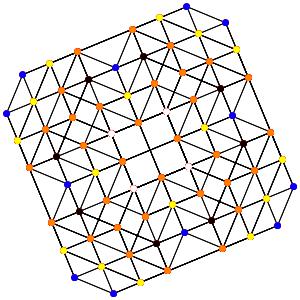
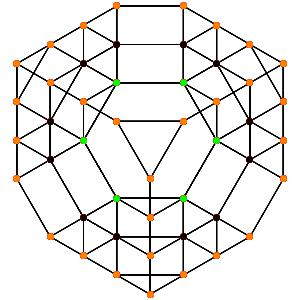
le t0123α5
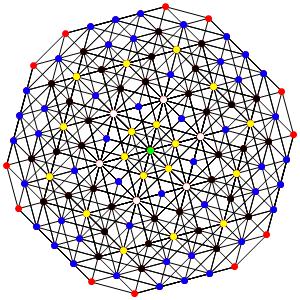
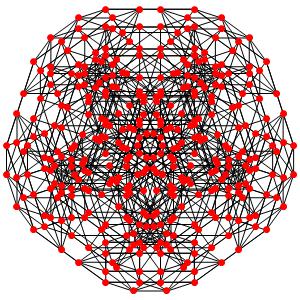
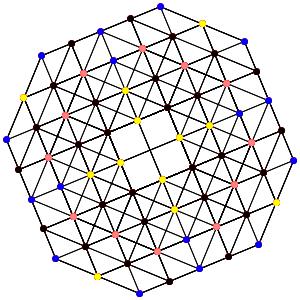
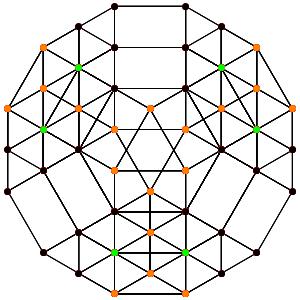
le t0234α5 Les points blancs sont 10-uples
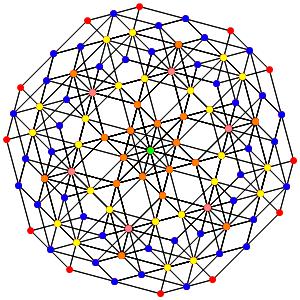
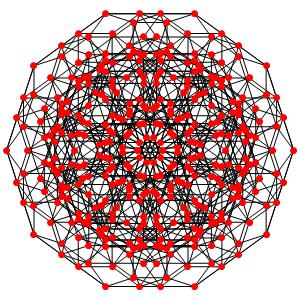
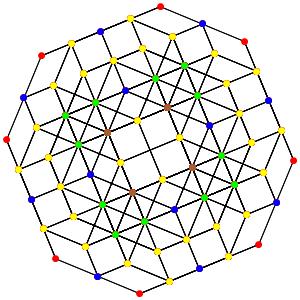
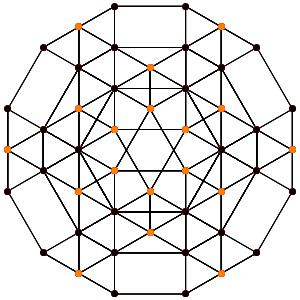
le t0134α5
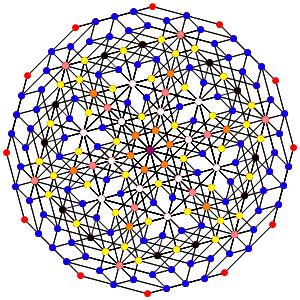
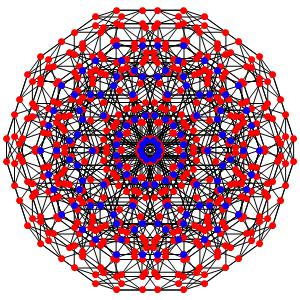
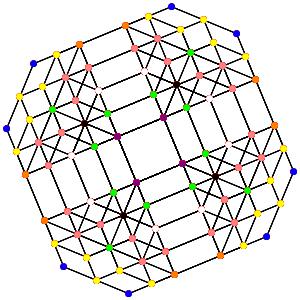
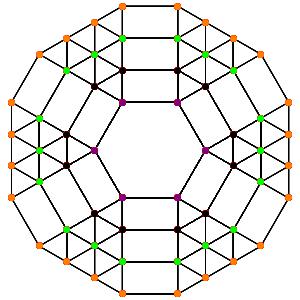
le t01234α5 Le point central est 24-uple
Pour la dimension 6 et au delà cela sera pour un autre jour!
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 204 autres membres