Polyèdres à la Renaissance
Un article de Jean-Jacques Dupas, cet article n'engage que son auteur
Les images de cet article sont, en général des images provenant d'autres sites
A la Renaissance il y a un intérêt renouvelé pour Platon et son « Timée », où les 5 polyèdres réguliers sont évoqués.
Au fronton de l'Académie (l'école fondée par Platon) on pouvait lire "que nul n'entre ici s'il n'est géomètre". Cette phrase résonne à la Renaissance. Les artistes de l'époque ne commencent leur formation artistique que quand ils maitrisent la géométrie. De plus dans le livre X de la République Platon oppose les Mathématiques représentant le vrai, à l'Art qui modifie les dimensions des objets pour les rendre plus vrais. Mais lisons Platon:
— Et les mêmes choses, quand on les regarde dans l’eau, ou à l’extérieur de l’eau, paraissent courbées, ou droites, et aussi creuses, ou bombées, à cause cette fois de l’illusion d’optique liée aux couleurs, et il est bien visible d que tout trouble de ce genre se situe à l’intérieur de l’âme. Or, c’est en exploitant cette sensibilité de notre nature que la peinture en trompe l’œil ne laisse rien à envier à la sorcellerie, comme le font aussi la démonstration de marionnettes et tous les autres procédés de ce genre.
— Oui, c’est vrai.
— Or, la mesure, le comptage, la pesée, ne sont-ils pas apparus comme les secours les plus bienfaisants contre ce risque, pour faire que ce qui dirige en nous soit, non pas l’apparence de grandeur, ou de petitesse, ou de nombre, ou de poids, mais l’élément qui se fonde sur le calcul et la mesure, ou bien encore sur la pesée ?
— Si, bien sûr.
— Mais cela, n’est-ce pas, c’est la fonction de l’élément qui, dans l’âme, est apte au calcul.
— Oui, c’est la sienne, en effet.
— Et pourtant il arrive souvent, quand il a mesuré et fait savoir que telles choses sont plus grandes ou plus petites que d’autres, ou égales à elles, que le contraire lui apparaisse en même temps, concernant les mêmes choses.
— Oui.
— Or, nous avons affirmé qu’il était impossible, au même élément, d’opiner en sens opposés sur les mêmes choses ?
— Et nous avons eu raison de l’affirmer.
— Par conséquent, l’élément de l’âme qui opine contrairement à l’opération de mesure ne saurait être le même que celui qui le fait en accord avec la mesure.
— Non, en effet.
— Mais, sans doute, celui qui fait confiance à la mesure et au raisonnement serait ce qu’il y a de meilleur dans l’âme.
— Oui, bien sûr.
— Par conséquent, celui qui s’oppose à ce dernier doit faire partie de ce qui, en nous, est de mauvaise qualité.
— Oui, nécessairement.
— Eh bien, c’est parce que je voulais nous faire tomber d’accord sur ce dernier point, que j’ai dit que l’art de peindre et en général l’art de l’imitation effectuait son ouvrage à distance de la vérité, et qu’au contraire c’est avec ce qui, en nous, est à distance de la réflexion qu’il était en relation, car il n’est le compagnon ni l’ami de rien de sain ni de vrai.
(source https://fr.wikisource.org/wiki/La_R%C3%A9publique_%28trad._Chambry%29/Livre_X)
La perspective de la Renaissance réconcilie les Arts avec les Mathématiques puisque avec les règles de la perspective il redevient possible de donner les dimensions d'un objet représenté.
La perspective s'appuie aussi sur les théories optiques du moyen-âge.
Par ailleurs à la Renaissance on connait bien les Éléments d'Euclide qui décrivent les 5 polyèdres réguliers dans le livre XIII. Par contre le travail d'Archimède sur les polyèdre semi-réguliers (je consacrerai un article entier pour définir le terme semi-régulier) n'est pas connu, son livre sur le sujet est perdu et les œuvres de Pappus (synagogè ou collections mathématiques paru vers 340), qui évoquent les travaux d'Archimède ne seront traduites en latin que dans d l'édition de Commandino de 1588.
La théorie de la perspective commence avec Filipio Bruneleschi(1377-1446) (à gauche sur l'image suivante) et Leon Battista Alberti(1404-11472)(à droite sur l'imàge suivante)


La première publication sur la perspective se trouve dans le Della Pittura d'Alberti en 1436
Paolo Ucello(1397-1479)
Il travaille sur la mosaique de la basilique Saint-Marc à Venise
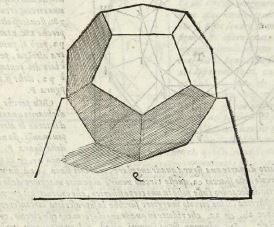
A ce titre on lui attribue la première instance du petit dodédécaèdre étoilé, Cf. figure ci-dessous

C'est Siegmund Günther qui dans un ouvrage de 1876 remarqua le premier cette instance du petit dodécaèdre étoilé à Saint-Marc de Venise, cette référence est donnnée dans "Imagine Math 3: Between Culture and Mathematics, Michele Emmer, Springer"
Malheureusement je n'ai pas trouvé trace de cette affirmation dans "Geschichte der Mathematischen Wissnschaften" de Siegmund Günther paru en 1876
Lucio Saffaro, aurait découvert dans la chapelle San Pantalon, de l'église San Pantalon à Venise deux autres pavages reprsésentant la deuxième étoile de Kepler, ces pavages auraient soufferts de la réfection de l'église depuis, mais auraient pu être l'oeuvre d'Ucello, chers lecteurs si vous passez par là....
Ce dodécaèdre étoilé est devenu célèbre car il fut le symbole de la biennale de Venise 1986
Paolo Ucello était fou de perspective, dans le livre de Vasari(1511-1574) "Les Vies des meilleurs peintres, sculpteurs et architectes" dans l'article sur Ucello il nous dit
"Paolo Uccello aurait possedé le talent le plus charmant et le plus inventif de la peinture depuis Giotto,s'il avait pris pour les figures
et les animaux autant de peine et de temps qu'il en perdit dans l'étude de la perspective"
plus loin il précise que quand Ucello montrait un mazzochio à son ami Donatello celui ci lui rétorquait :
"Ah ! Paolo, tu laisses la substance pour l’ombre ! »
Donatello lui reprochait de trop travailler sur la perspective, le mazzochio, les sphères à 72 faces et qu'il aurait dû laissé cela aux spécialiste de l'intarsia
Le mazzochio est un tore à facettes objet de prédilection des spécialistes de la perspective
en voici des exemples réalisés par Paolo Ucello:

Voici un dessin conservé au musée du Louvres

Un autre exemple (Galleria degli Uffizi, Gabinetto dei Disegni)
Ce thème du mazzochio apparait dans plusieurs oeuvres de Paolo Ucello.

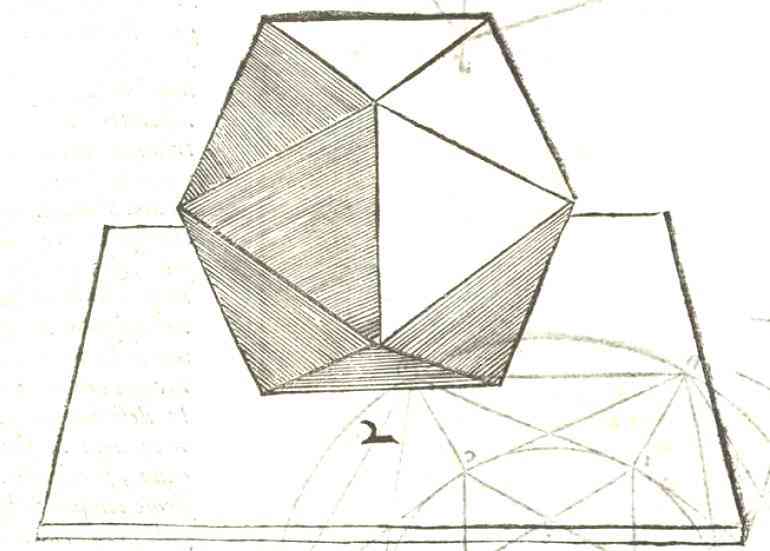
Voici la fameuse sphère avec des piques(preuve que l'idée d'ériger des pyramides sur les faces d'un polyèdre est assez ancienne)

Intarsia
Il y a eu avec les début de la perspective une folie de l'intarsia, en particulier à Florence où l'on comptait plus de 84 échoppes en 1478.
Mais qu'est-ce que l'intarsia? Ce sont des panneaux de bois en marqueterie qui représente des trompe-l’œil en perspective, typiquement des porte de placard qui représentent des portes de ces placards ouvertes avec des objets où des scènes à l'intérieur. Parmi les objets privilégiés des polyèdres, des sphère de Campanus, des mazzochi.
Les intarsiatori étaient des maîtres de la perspective.
Pourquoi l'intasia est-elle importante dans l'histoire des polyèdres ?
Car par exemple Lorenzo da Lendinara, reconnu de son temps comme un intarsiatori de premier plan était le parrain de Luca Pacioli et à enseigné à Piero della Francesca. Cet art était situé entre la menuiserie, l'ébénisterie et la marqueterie, les artistes ont certainement construit de vrais polyèdres en bois qui ont aidé à la compréhension de la géométrie.
L' intarsiatori le plus célèbre était Fra Giovanni. Le pape Jules II, un ami de Luca Pacioli, lui commenda les panneaux qui décorent la Stanza della Segnatura, où se trouve aujourd'hui le tableau l' ( Ecole d'Athène). Il ne reste plus que 4 panneaux aujourd'hui.
Voici les panneaux qui se trouvent au monastère de Monte Olivetto Maggiore à côté de Sienne


Sur le panneau de gauche un icosaèdre tronqué, un icosaèdre, une sphère de Campanus
Sur le panneau de droite un icosidodécaèdre sommé de pyramides, un cuboctèdre, un cube sommé de pyramides

un mazzocchio, une sphère de campanus
Sur ce site : Monte Oliveto Il y a de meilleures images.
Un autre panneau qui se trouve dans l'église san Domenico de Bologne avec un petit rhombi cuboctaèdre en bas à gauche

un autre panneau attribué à Fra Damiano da Bergamo au musée de l'église San domenico de Bologne

Le polyèdre représenté au centre me parait curieux! Ce n'est pas un nouveau polyèdre archimédien car je pense que ce solide n'est pas convexe.Il y a un icosidodécaèdre au dessus et deux cuboctaèdres avec des pyramides ajoutées sur les faces. Notez que sur ces deux polyèdres étoilés si les pyramides sur les faces carrées s'alignent pour former un octaèdre à gauche, celles sur les triangles, à droite, sont trop hautes et ne forment pas un cube c'est domage! la figure eut été géniale!
un autre panneau toujours au musée de l'église San Domenico de Bologne attribué à Fra Damiano da Bergamo

Un panneau avec un mazzocchio, une sphère armilaire et un astrolabe, au palais ducale d'Urbino

L'intarsia a disparu vers 1550 aussi vite qu'elle était apparue, delaissée car considérée comme une technique au profit de la peinture considérée comme un art
Piero della Francesca(1412-1492)

Portrait de Piero della Francesca, attribué à Santi di Tito, en mathématicien, remarquez les oeuvres d'Euclide et d'Archimède sur la table, bien que Piero ne connaisse pas les travaux d'Archimède sur les polyèdres.
Pierro della Francesca était l'aîné (des enfants survivants) d'un marchand prospère de Borgo San Sepolcro, dans la vallée du Tibre en Toscane.
Il a montré des dons évidents pour les mathématiques dans sa jeunesse, qui le poussèrent à rédiger des traités de mathématiques pour son usage propre.
Il a été l'élève de Lorenzo da Lendinara à Rome un intartiatoti réputé de son temps
d'après Vasari: "Piero, comme nous l'avons dit, était grand travailleur. Il s'appliqua beaucoup à la perspective et étudia profondément Euclide. C'est à lui que l'on doit les meilleures notions sur la géométrie."
Son œuvre mathématique est injustement méconnue, c'était le meilleur géomètre de son époque, il a pratiquement inventé le dessin technique. Ses œuvres n'ont pas été publiées de son vivant sous son nom. C'est peut-être pour cela qu'il est moins connu. Nous ne savons pas s'il était capable d'écrire en latin.
Deux de ses œuvres nous intéressent le Trattato d'Abaco (traité de l'abaque) et le Libellus de Quinque Corporibus Regularibus (petit livre sur les cinq solides réguliers)
Dans le Trattato nous trouvons une description du tétraèdre tronqué et du cuboctaèdre, le Trattato contient beaucoup plus de géométrie que les traités du même type de l'époque.
la partie géométrique du Trattato commence avec un chapitre sur les triangles et des questions pratiques sur la détermination des aires de triangles.
Puis il passe à la géométrie solide avec le tétraèdre et le cube avec des références au livre 13 des Eléments d'Euclide.
Il arrive à la sphère avec des problème du type
Soit une sphère de diamètre 7, je veux y inscrire une figure constituée de 4 triangles équilatéraux (tétraèdre) de sorte que les sommets touchent la sphère. Quel est le côté du triangle?
Il introduit alors un nouveau solide:
Soit une sphère de diamètre 6, je veux y inscrire une figure constituée de 8 faces :4 triangles équilatéraux et quatre hexagones Quel est le côté du triangle?

Le tétraèdre tronqué du trattto
Soit une sphère de diamètre 6, je veux y inscrire une figure constituée de 14 faces :8 triangles équilatéraux et six carrés, tous les côtés sont égaux. Quel est le côté?
Le cuboctaèdre du trattato
Dans le Libellus de Quinque Corporibus Regularibus on trouve tous les 5 polyèdres tronqués et le cuboctaèdre.
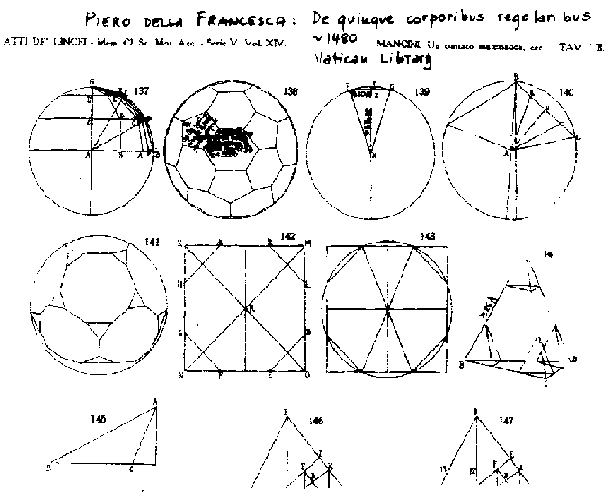
Une des rares planches visible sur internet un icosaèdre tronqué 138, un dodécaèdre tronqué 141, un cube tronqué 142, un tétraèdre tronqué à droite au milieu

Une page du Libellus de Quinque Corporibus Regularibus où les illustrations seraient de Piero della francesca lui-même, à gauche l'inscription d'un icosaèdre dans un cube et à droite l'inscription d'un cube dans un octaèdre.
Piero della Francesca a bien fait la différence entre la troncature au milieu de l'arête qui donne le cuboctaèdre des troncatures conduisant aux solides tronqués, il est le premier à la Renaissance à avoir utilisé la troncature pour construire de nouveaux polyèdres et à surtout à l'avoir comprise.
Piero della Francesca a relancé l'étude des polyèdres à la Renaissance, par son travail aussi bien sur les polyèdres que sur la perspective, il a été source d'inspiration pour de nombreux contemporains.
Polyèdres archimédiens décrits par Piero della Francesca
- Tétraèdre tronqué (Libellus, Trattato)
- Cube tronqué (Libellus)
- Octaèdre tronqué (Libellus)
- Dodécaèdre tronqué (Libellus)
- Icosaèdre tronqué (Libellus)
- Cuboctaèdre (Trattato)
Luca Pacioli (1445-1514)

Luca Pacioli au centre, remarquez le petit rhombiCuboctaèdre en verre, à moitié rempli d'eau en haut à gauche, le petit rhombiCuboctaèdre est le symbole de Luca Pacioli, ses admirateurs lui en attribue la paternité, un dodécaèdre est posé sur le best-seller de Luca Pacioli Summa de arithmetica, geometria, de proportioni et de proportionalita.
L'oeuvre la plus connue de Luca Pacioli est « de divina protortione » , cet ouvrage a été beaucoup mis en avant par les adorateurs du nombre d'or. Une première remarque sur le nom de cet ouvrage. Dans le Timée, Platon associe les 4 éléments à 4 des 5 solides réguliers, je ne reviens pas sur cette association mystique, je rappelle que notre monde est constitué d'atomes. Mais comme il y a 5 solides, le cinquième, qui n'est pas décrit, juste évoqué dans le Timé, est associé à l'univers, aux cieux, au divin. La divine proportion est donc la proportion qui permet de construire le solide associé au divin. Le dodécaèdre régulier est donc dans son abstraction, figure éternelle et parfaite, une représentation de Dieu. Le nombre d'or était connu d'Euclide comme la proportion qui découpe un segment en extrême et moyenne raison donc rien de bien neuf.
de divina protortione est divisé en 3 parties:
-
Un texte de Luca Pacioli, assez laconique qui renvoie souvent aux figures, ce texte est assez faible mathématiquement.
-
Des illustrations extraordinaires de Léonard de Vinci (ces figures en montre plus que le texte de Pacioli)
-
Une version en italien du Libellus de Quinque Corporibus Regularibus de Piero della Francesca
Au départ ce texte ne devait pas être publié, il doit son succès, en grande partie, à cause des illustrations de Léonard de Vinci, c'est le premier livre imprimé où l'illustrateur est bien meilleur que l'auteur !
Il existe une polémique autour de la troisième partie qui est une version en italien du Libellus de Quinque Corporibus Regularibus de Piero della Francesca, or celui-ci n'est pas cité, c'est pour cela que Luca Pacioli a été accusé de plagiat. Comme c'était un ami de Piero della Francescail a peut être simplement voulu que le texte de son ami soit publié et passe à la postérité.
Autre fait plus troublant, alors qu'il connaissait bien Piero della Francesca, certains polyèdres qui apparaissent chez Piero della Francesca ne sont pas décrit chez Luca Pacioli, comme le cube tronqué et le dodécaèdre tronqué. En particulier, Piero della Francesca, fait la clairement la différence entre la troncature qui transforme les n-gones initiaux en 2n-gones (les triangles du tétraèdre, octaèdre, icosaèdre en hexagones, les carrés du cube en octogones, les pentagones du dodécaèdre en décagones) de la troncature au milieu des arêtes qui conduit au cuboctaèdre.
Le tétraèdre tronqué, l'octaèdre tronqué et l'icosaèdre tronqué dessiner par Léonard de Vinci dans de divina protortione
C'est moins clair chez Luca Pacioli son cubus abscisus est le cuboctaèdre comme son dodecaedron abscisus qui est l'icosidodécaèdre (non connu de Piero della Francesca), alors que son tetraedron abscisus est le tétraédron tronqué, son octaedron abscisus est l'octaèdre tronqué.
Le cuboctaèdre et l'icosidodécaèdre dessiner par Léonard de Vinci dans de divina protortione. Pour l'icosidodécaèdre c'est la première représentation connue.
Un nouveau polyèdre apparaît chez Luca Pacioli, le petit rhombicuboctaèdre. Entre parenthèses, le nombre d'or n'intervient pas dans la construction de ce solide. Il est nommé vingintisex basium (26 faces) et obtenu par troncature du cuboctaèdre au milieu des arête. Si on pratique réellement cette troncature on obtient des rectangles et non pas des carrés supplémentaires, il faut faire des ajustements pour obtenir des carrés.
La vraie troncature du cuoctaèdre donne des rectangles ici verts, modèle construit par Jean-Jacques Dupas
Cette méprise a conduit Luca Pacioli à penser que l'on pouvait construire autant de solides semi-réguliers que l'on voulait par troncatures successives. Ce qui prouve que Luca Paciloli ne connaissait pas Pappus et explique pourquoi il n'a pas cherché à donner une liste exhaustive de polyèdres semi-réguliers. Faut-il attribuer cette découverte à Pacioli, à Léonard de Vinci ?
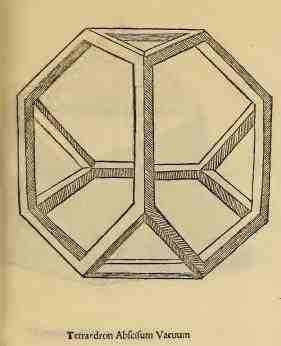
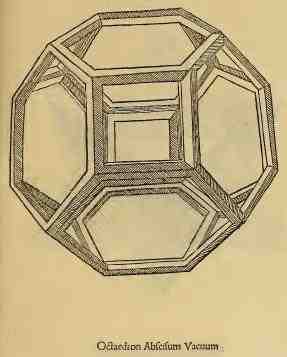
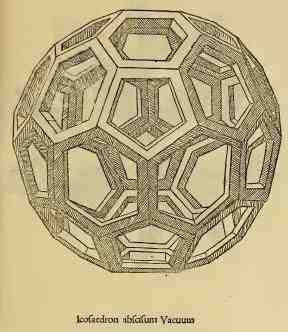
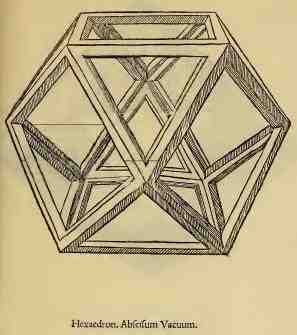
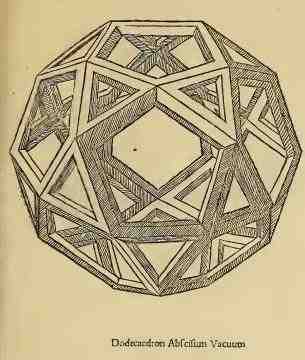
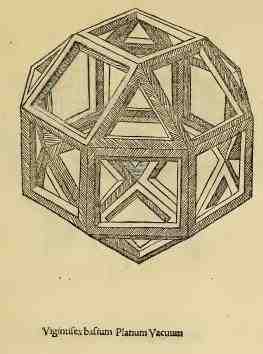
Le solide à 26 faces dessiner par Léonard de Vinci dans de divina protortione version solidum à gauche et vaccum à droite
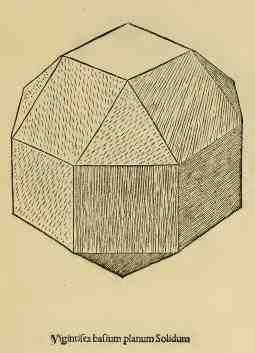
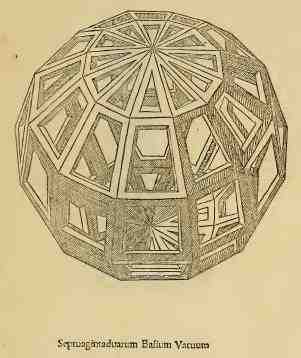
Quoi qu'il en soit, dans son portrait, ce solide apparaît comme son symbole. Luca Pacioli prédit que ce polyèdre serait utile aux architectes. Ceux-ci ne l'on visiblement pas beaucoup écouté. Luca Pacioli décrit aussi un solide à 72 faces, connu de Piero della Francesca, qui servira de support à la construction de coupoles.
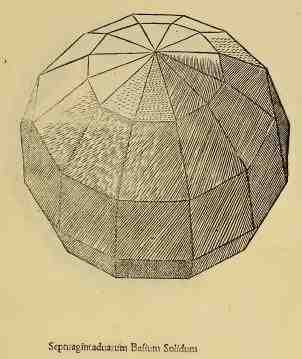
Le solide à 72 faces dessiner par Léonard de Vinci dans de divina protortione version solidum à gauche et vaccum à droite
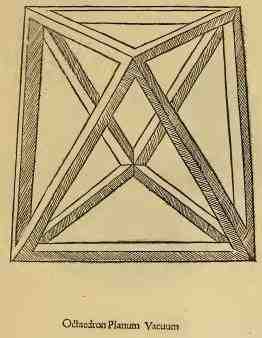
Dans de divina protortione chaque solide est décliné sous quatre formes :
-
solidum (plein)
-
vaccum (évidé, comme s'il était construit avec des barraux prismatiques en bois)
-
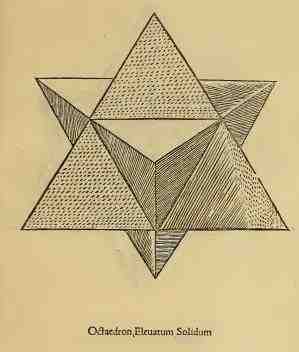
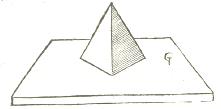
elevatum solidum (plein, une pyramide régulière pleine est érigée sur chaque face du polyèdre de base)
-
elevatum vaccuum (évidé, une pyramide régulière évidée est érigée sur chaque face du polyèdre de base)
Un octaèdre dessiner par Léonard de Vinci dans de divina protortione version solidum à gauche, puis vaccum, puis elevatum solidum enfin elevatum vacuum, l'octaedron elevatum sera plus connu sous le nom de stella octangula donné par Kepler
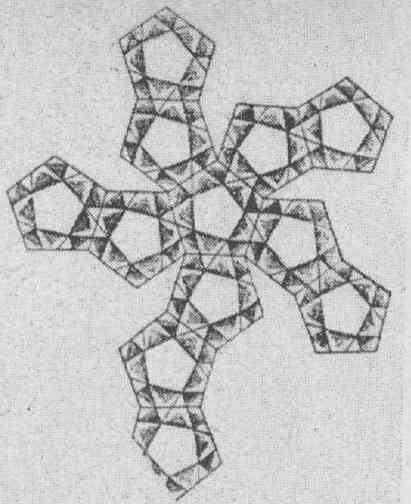
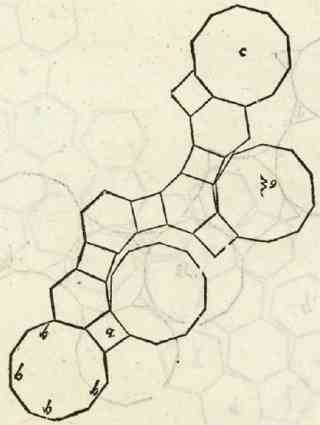
Dans l'article New light on the rediscovery of the Archimedean solids during the Renaissance de Peter Schreiber, Gisela Fischer ·et Maria Luise Sternath, les auteurs nous signalent que les reproductions du de divina proportione ne montrent pas tous les dessins en particulier ils ne reproduisent que rarement les patrons de polyèdres ? Ce qui ferait de Léonard le précurseur de l'utilisation des Patrons avant Dürer. Voici un exemple tiré de cet article :
On pourrait croire que ce n'est que le patron d'un dodécaèdre, avec des décorations. En fait c'est certainement un cube camus, nous verrons cela dans l'article Polyèdres à la renaissance : une surprise. Si quelqu'un sait comment obtenir les images manquantes du de divina proportione je suis preneur.
Pour continuer sur Léonard, l'article de "Pour la Science" de Loic Mangin L'erreur de Léonard de Vinci, Signalait que D.Huylebrouck avait repéré une erreur sur la version elevatus du solide à 26 faces.
Dans un autre article de Jörg M.Wills, Leonardo and the pseudo-RCO examine l'hypothèse suivant laquelle le solide représenté serait la version elevatus du pseudo-petit-rhombi-cuboctaèdre, le quatorzième solide archimédien dont je reparlerai et que donc il n'y aurait pas d'erreur, faisant du coup de Léonard l'inventeur de ce solide dont plusieurs auteurs du XXème siècle se disputent la paternité.
Albrecht Dürer (21/05/1471-06/04/1528)
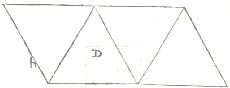
Dans l'édition de Nuremberg de 1525 de "Underweysung der Messung mit dem Zirkel und Richtscheyt" les 5 solides de Platon apparaissent en perspective et sous formes de patron. Il semble que l'utilisation des patrons soit une inovation de Dürer (affirmation faite avant Polyèdres à la renaissance : une surprise.). Dans cette édition on trouve aussi le tétraèdre tronqué et tous les polyèdres archimédiens du groupe du cube mais uniquement sous forme de patrons, donc deux nouveaux polyèdres le grand-rhombi-cuboctaèdre et le cube camus. Dans l'édition posthume augmenté de 1538 on trouve aussi l'icosaèdre tronqué et l'icosidodécaèdre toujours sous forme de patrons. Dürer ne donne pas ses sources.
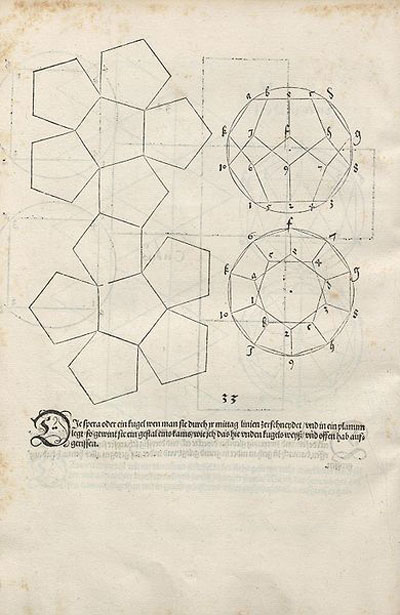
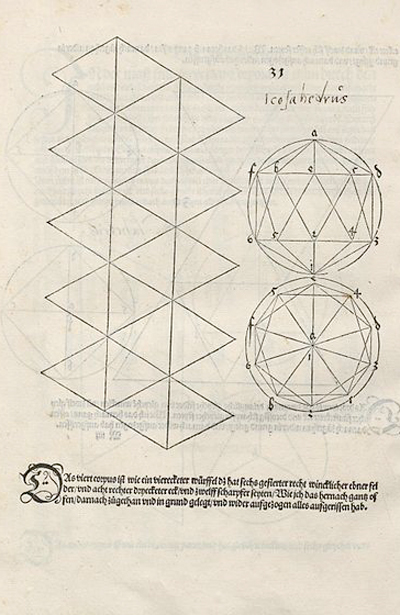
Un dodécaèdre et son patron à gauche à droite un icosaèdre et son patron
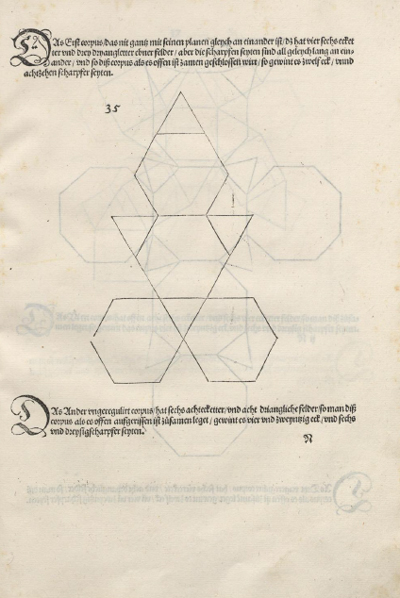
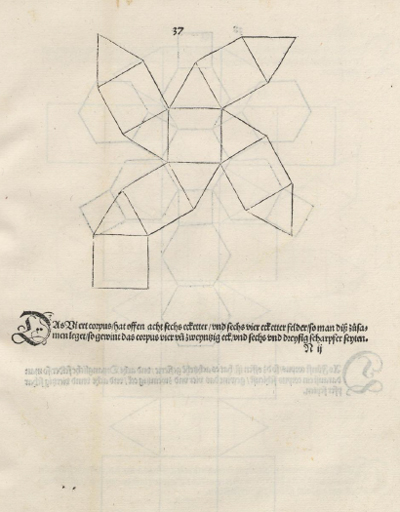
Le patron d'un tétraaèdre tronqué à gauche le patron d'un cuboctaèdre à droite
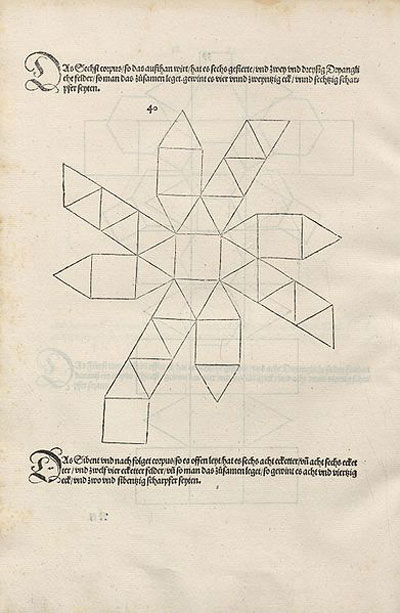
Le patron du cube camus, C'était une bonne idée de passer par le patron car ce polyèdre n'est pas constructible simplement !
L'article New light on the rediscovery of the Archimedean solids during the Renaissance de Peter Schreiber, Gisela Fischer ·et Maria Luise Sternath, nous propose plein de nouveautés sur les polyèdres à la Renaissance.Surprises
Daniele Barbaro (1514-1570)

Daniele Barbaro en officier de la chancellerie par Paul Véronese, sur la table deux de ses ouvrages, debout La pratica della perspettiva et posé son ouvrage sur l'architecture de Vitruve
Il rédigea La pratica della perspettiva(1568) dans lequel on trouve les polyèdres réguliers et archimédiens sous forme de patrons et de vues en perspectives. Mais pas tous, il ne manque que le cube camus et le dodécaèdre camus. Ces deux polyèdres ne sont pas constructibles à la règle et au compas ,de plus il y a plusieurs faux polyèdres.
Daniele Barbaro fit des contributions originales, ce fut le premier à écrire que le cuboctèdre pouvait aussi bien être deduit du cube que de l'octaèdre, c'est lui qui a montré le premier un petit rhombicosidécaèdre en perspective, c'est aussi lui qui parle du grand rhombicosidécaèdre en premier, pour ce dernier qu'il décrit avec justesse il ne donne qu'un morceau de patron
quelques images tirées du La pratica della perspettiva
Un des patrons du tétraèdre
Le tétraèdre en perspective
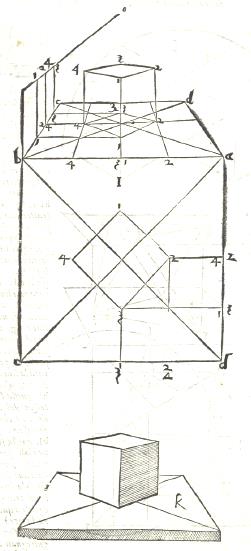
un des patrons du cube
Un cube en perspective
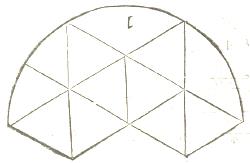
Un des 11 patrons de l'octaèdre
Un dodécaèdre en perspective
Un icosaèdre régulier en perspective
le premier petit rhombicosidécaèdre en perspective de l'histoire!
Un morceau du patron du premier grand rhombi-cuboctaèdre de l'histoire !
Après avoir donné les patrons de quelques faux polyèdres, Barbaro arrive même à en construire un en perspective! (comme quoi il faut se méfier des dessins)
Il donne des patrons de solides du type "elevatus" c'est-à-dire des solides sommés sur toutes les faces de pyramides régulières. Puis il présente la construction de mazzocchio.
Références:
Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler. J.V. Field, Archive for History of Exact Sciences Vol. 50, No. 3/4 (September 1997), pp. 241-289
Renaissance Intarsia: The art of geometry, Alan Tormey, Judith farr Tormey, Scientific American, 1982, n° 247, p136-147
New light on the rediscovery of the Archimedean solids during the Renaissance de Peter Schreiber, Gisela Fischer ·et Maria Luise Sternath
L'erreur de Léonard de Vinci, Loïc Mangin, Pour la Science, n°404, juin 2011
D.Huylebrouck, Een fout van Leonardo da Vinci, EOS, avril 2011
Jörg M.Wills, Leonardo and the Pseudo-RCO
Carlo H. Sequin "Lost in Triangulation" ?? No, -- it is not a mistake, -- it is a Pseudo Rhombicuboctahedron!
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 204 autres membres