PlayMaths : Changeons les Maths pour plus de plaisir

Un article de Jean-Jacques Dupas qui n'engage que son auteur

Cet article est un complément à l'article Polyèdres à la Renaissance

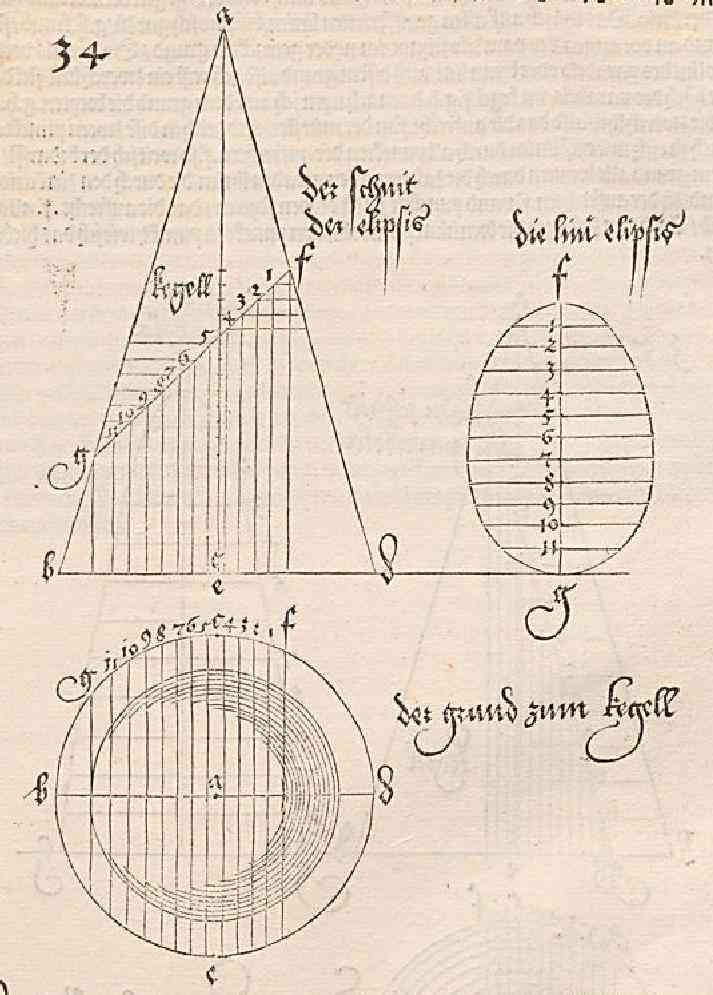
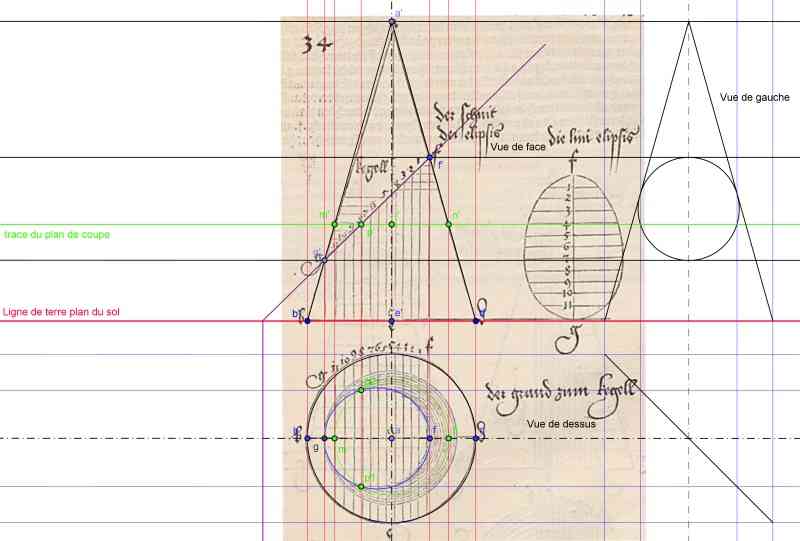
Aujourd’hui je vais vous apprendre à construire une ellipse en suivant la méthode d’Albrecht Dürer (1471-1528). On attribue l’invention du dessin technique à Piero della Francesca(1415-1492) (Cf. Piero della Francesca, peintre mathématicien, Enrico Gamba, Vico Montebelli, Pour la Science n°224 juin 1996, pp. 68-75), il en aurait jeté les bases dans son De prospectiva pigendi. Cependant il semble que ce soit Albrecht Dürer qui le premier utilisa cette technique du dessin technique pour obtenir des résultats mathématiques dans son « Underweysung der Messung mit dem Zirkel und Richtscheyt » (Instructions pour la mesure, à la règle et au compas, des lignes, des plans, et corps solides) publié en 1525 à Nüremberget, en particulier construire des coniques en coupant un cône de révolution (Cf. Les coniques suivant Dürer, Daniel Silver, Pour la Science n°425 mars 2013, pp.74-78). Voici le dessin de Dürer, je vais vous montrer comment faire le même et vous expliquer comment grâce aux techniques du dessin industriel et de la géométrie descriptive on peut le comprendre.

Figure 1 : la figure d’Albrecht Dürer pour la construction de l’ellipse

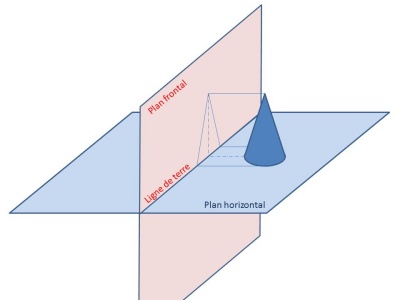
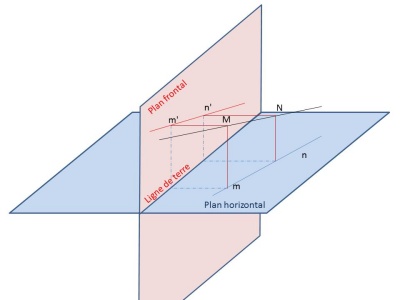
La géométrie descriptive a été formalisée par Gaspard Monge (1746-1818). elle est la base théorique du dessin technique. En géométrie descriptive, on utilise deux plans de projection orthogonaux qui sont le plan horizontal et le plan frontal. Sur le plan frontal nous aurons la vue de face et sur le plan horizontal la vue de dessus.

Figure 2 : les plans de projection

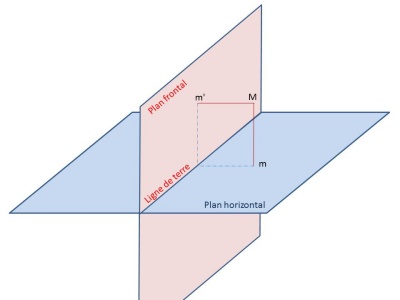
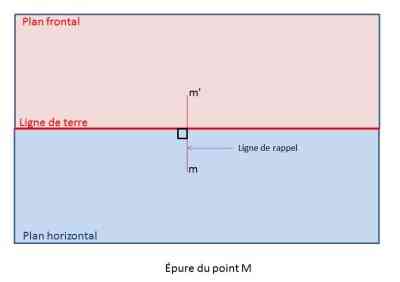
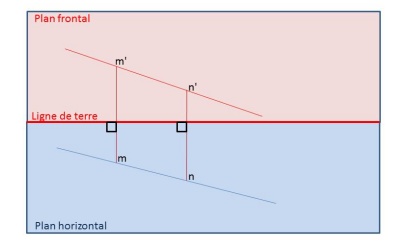
Figure 3 : Un point M possède une projection sur le plan frontal m’ et une projection sur le plan horizontal m, sur l’épure à droite m' et m sont reliés par une ligne de rappel (en géométrie descriptive les lignes de rappel sont en « carmin fin » en dessin technique la ligne de rappel est effacée pour le rendu final)

Figure 4 : épure d’une droite

Nous refaisons la figure

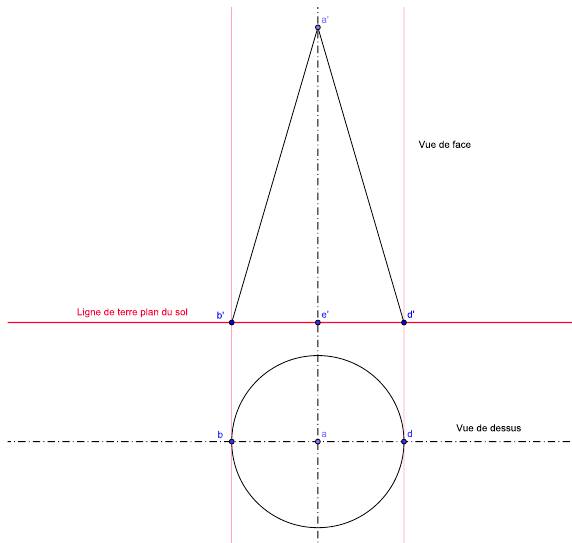
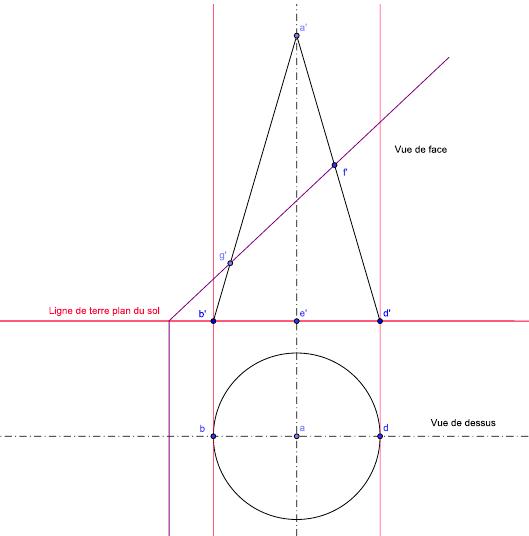
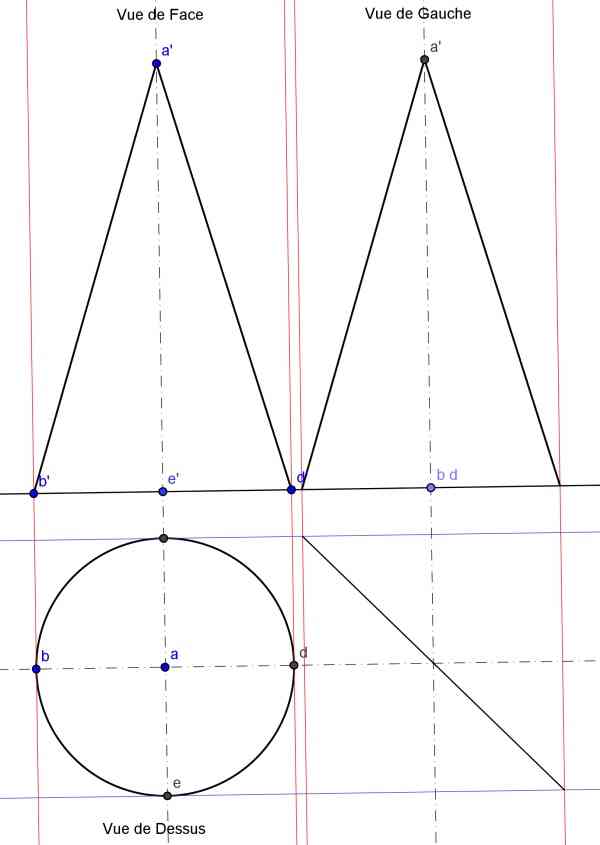
On commence par la mise en place de la ligne de terre. Puis, en vue de face le cône sera vu comme le triangle a’, b’, d’. Pour la vue de dessus, c’est-à-dire la projection dans le plan horizontal, on choisit un axe parallèle à la ligne de terre, sur cet axe on reporte a, b, d. Il ne nous reste plus qu’à tracer la base du cône, le cercle de centre a et de diamètre b, d.

Figure 5 : mise en place du cône

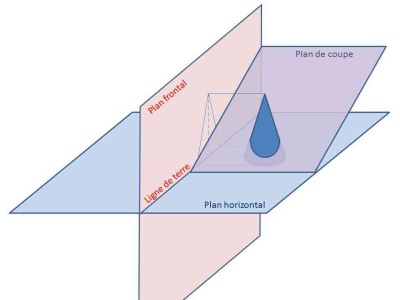
Nous allons couper notre cône par un plan. L’astuce de Dürer est de couper le cône par un plan orthogonal au plan frontal. Il sera donc vu en vue de face de bout, sa trace sur le plan horizontal sera une droite orthogonale à la ligne de terre.

Figure 5 : mise en place du plan de coupe

Figure 6 : épure du cône avec son plan de coupe

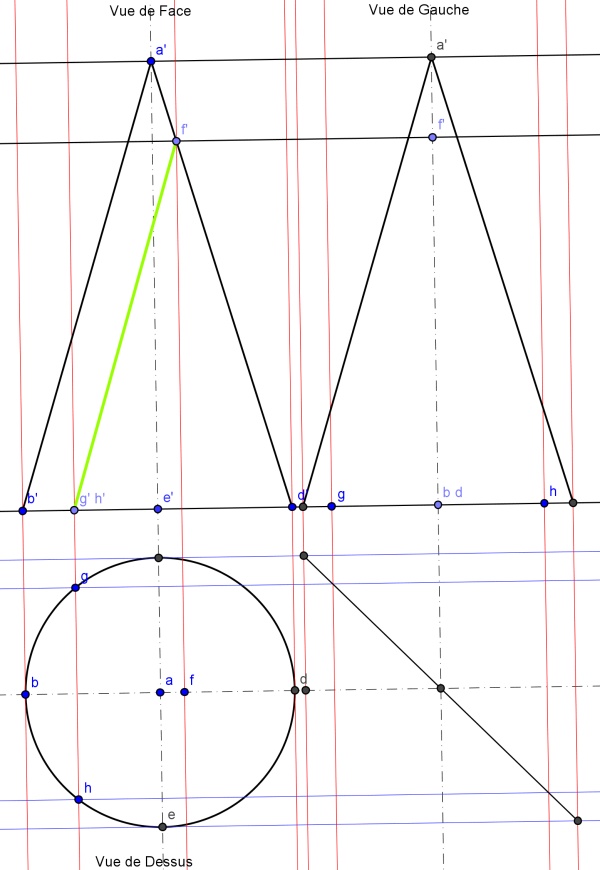
Nous pouvons déterminer les deux points de l’intersection en reportant f’ et g’ en vue de dessus sur l’axe (b, d).

Pour obtenir ces deux points nous utiliserons un cas particulier de l’utilisation d’un plan auxiliaire horizontal.

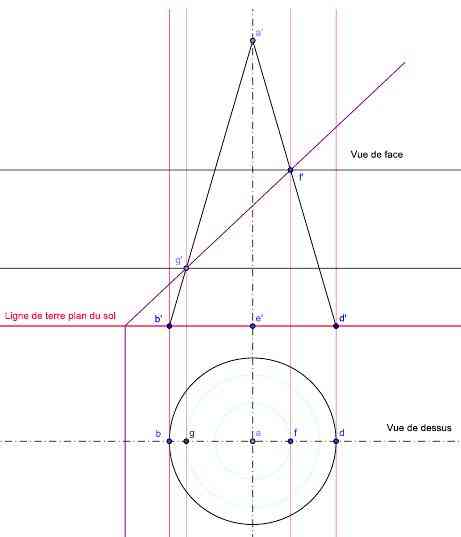
Prenons un plan horizontal passant par f’ nous le voyons en vue de face comme un trait noir parallèle à la ligne de terre. En vue de dessus ce plan coupe le cône suivant un cercle bleu clair de centre a et de rayon [a, f] l’intersection de ce cercle avec la ligne de rappel issue de f’ nous donne un point unique f, le même raisonnement avec le point g’ nous donne le point g.

Figure 7 : construction des deux premiers points

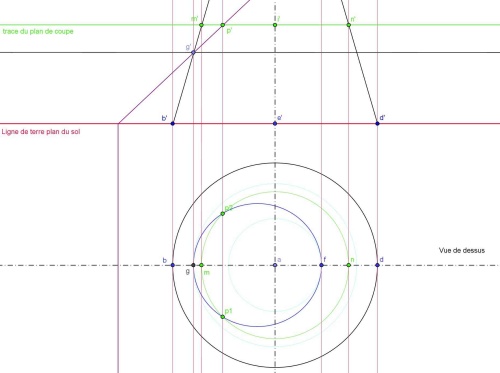
Nous allons nous servir d’un plan de coupe auxiliaire horizontal générique parallèle au sol, ce plan passe par le point i’ sur la vue de face, comme c’est un plan horizontal sur la vue de face c’est un plan vu de bout donc nous ne voyons que sa trace verte, en vue de face ce plan coupe le cône en deux points m’ et n’, reportons ces points sur la vue de dessus en m et n. Le cône est coupé par ce plan auxiliaire suivant un cercle vert dont le diamètre est [m, n].

Ce plan auxiliaire coupe aussi le plan de coupe, cette intersection est une droite vue de face, elle est vue de bout elle passe par p’, en vue de dessus c’est une droite perpendiculaire à la ligne de terre. L’intersection du plan auxiliaire et du cône étant le cercle de diamètre [m, n], l’intersection du plan auxiliaire et du cône est l’intersection de cette droite perpendiculaire à la ligne de terre et du cercle de diamètre [m, n] soit les points p1 et p2. Nous avons deux points de notre ellipse. En prenant autant de plans auxiliaires que nécessaire à la précision du tracé, nous obtenons notre ellipse bleu en vue de dessus. Dürer a utilisé 11 plans auxiliaires.

Figure 7 : construction du point courant

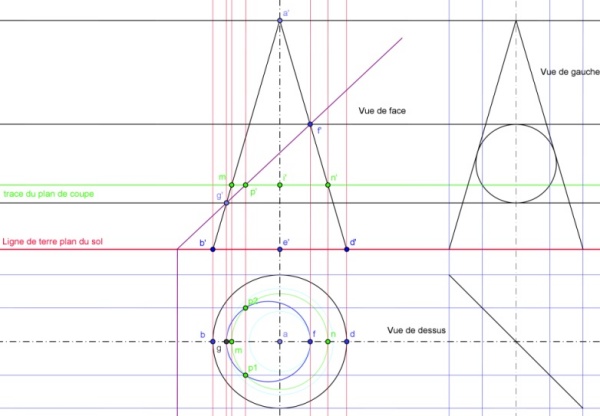
On peut construire une vue de gauche, c’est-à-dire une projection dans un plan orthogonal au plan frontal et horizontal, la seule concession au modernisme est l’utilisation d’une droite à 45° en bas à droite pour reporter les distances.

Figure 8 : construction de la vue de gauche

On s’aperçoit que Dürer à fait de bonnes constructions, mais curieusement son résultat final est faux il n’obtient pas une ellipse mais un œuf. Remarquez dans melancholia la forme de la cloche on retrouve une forme ovoïde.

Figure 9 : Détail de melancholia de Dürer

Figure 8 : notre construction et celle de Dürer

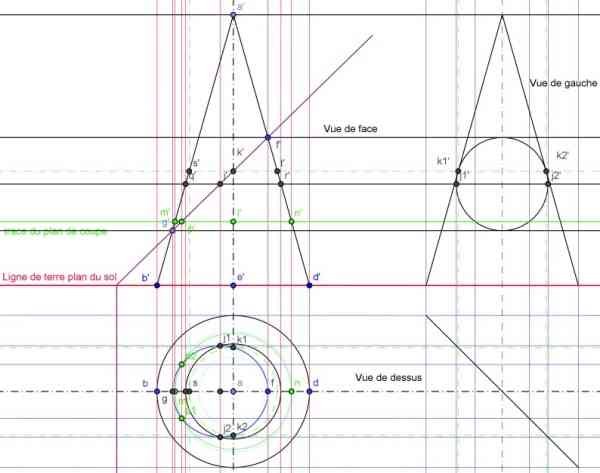
Maintenant il y a plus rigolo à faire, déterminer les tangentes particulières

Sur la vue de dessus les tangentes verticales se trouvent en f et g pour une raison de symétrie par rapport à l’axe. Toujours pour des raisons de symétrie si on utilise le plan horizontal auxiliaire passant par j’ milieu de [f’, g’] on obtient les points j1 et j2 des tangentes horizontales à l’ellipse sur la vue de dessus et les points j1’ et j2’ des tangentes verticales sur la vue de gauche.

Maintenant si on prend le plan horizontal auxiliaire passant par k’ intersection du plan de coupe avec l’axe du cône, cela nous donne en vue de gauche k1’ et k2’ lieu où la tangente à l’ellipse est sur les génératrices extérieures au cône dans cette vue.

 Figure 8 : constructions des tangentes

Prochainement nous verrons la parabole et l'hyperbole qui sont bien construites par Dürer

Chose promise, chose due je vous montre la construction de la parabole le 19 mai 2016

Mise en place du cône

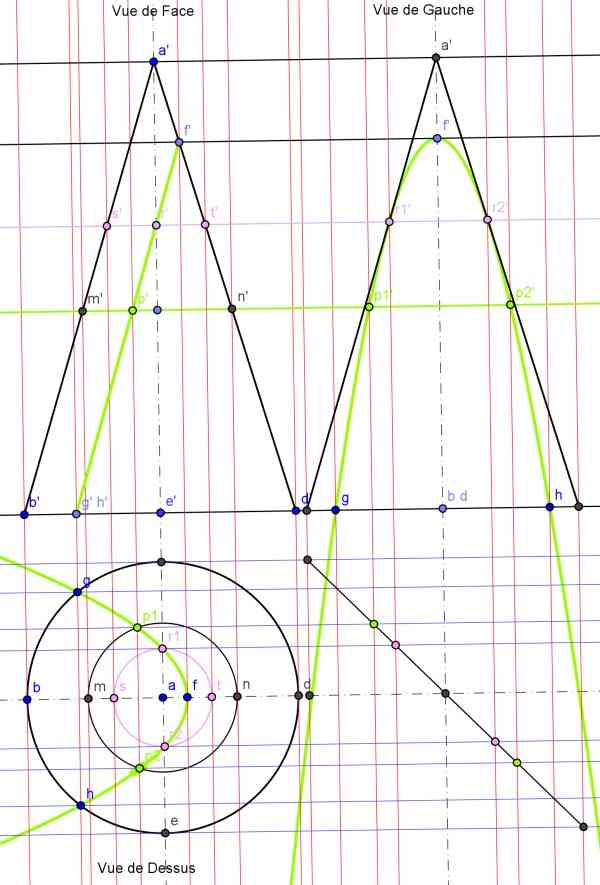
mise en place du plan de coupe en vert, il est vu de bout sur la vue de face

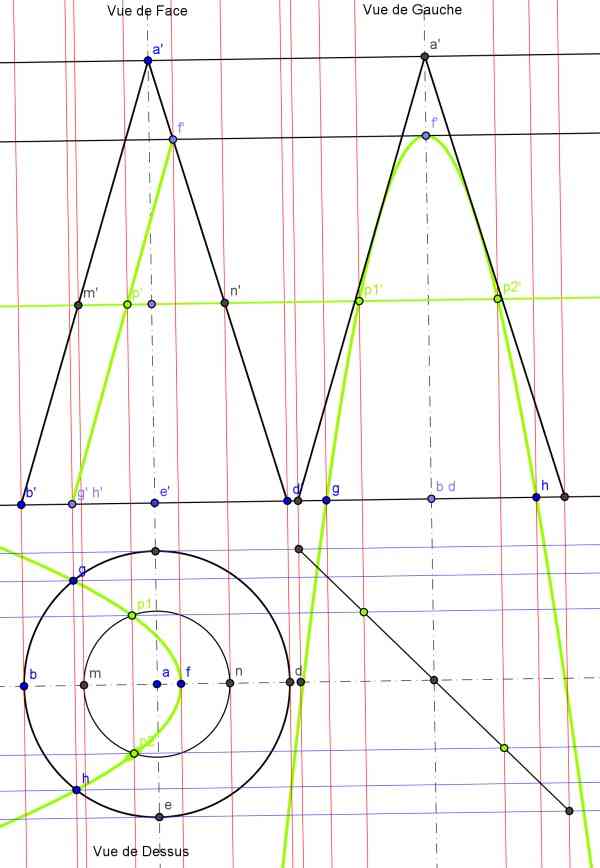
Construction du point courant en s'aidant d'un plan horizontal, passant par MN. Sur la vue de face on coupe le plan en p', on reporte en vu de dessus d'où p1 et p2, qui sont reportés en vue de gauche d'où 2 points p1' et p2' on refait cette opération autant que la précision du tracé le requiert

Tracé des point où la parabole est tangente au cône en vue de gauche. C'est la même construction que la précédente sauf que l'on part en vue de face du point où le plan coupe l'axe du cône.

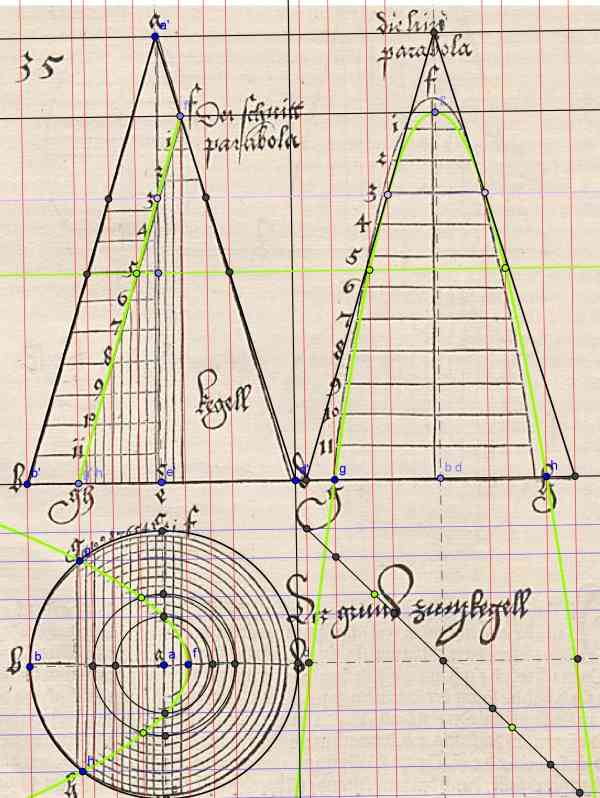
Ma construction et celle de Dürer, cette fois ci la construction est juste

Puis Dürer construit une hyperbole mais cela sera pour un autre jour